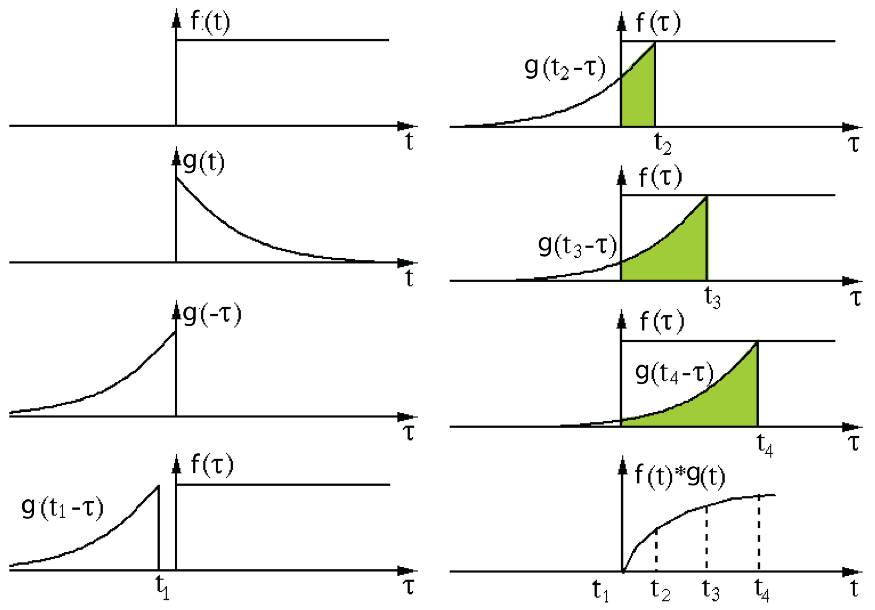
کانولوشن (convolution) و قضیه کانولوشن
در مقاله پیش رو که برگرفته از وبلاگ سیگنالهای ایستان چرخشی (Cyclostationary) است و توسط آقای اسپونر (Spooner) نوشته شده است، مباحث مهمی درباره کانولوشن مطرح شده و تصاویر و ویدئوهای جالبی نیز در این ارتباط از طریق کدنویسی متلب توسط ایشان تولید شده است. در انتها نیز لینک مقاله و همچنین لینک وبلاگ برای مطالعه بیشتر آورده شده است.
کانولوشن یک بخش اساسی در جعبه ابزار پردازش سیگنال برای هر متخصصی در این زمینه است. در این مقاله به جزییات این موضوع مهم خواهیم پرداخت. موضوع کانولوشن از سری مقالات مربوط به پردازش سیگنال است که همه جا دیده میشود. قبلا این موضوع در رابطه با سیستمهای خطی تغییر ناپذیر با زمان مطرح شده است. در این مقاله، تمرکز بر روی جزییات عملیاتی محاسبه کانولوشن و بحث در مورد کاربرد موثر آن در پردازش سیگنال است.
مروری بر ریاضیات کانولوشن
انتگرال کانولوشن، که برای سیگنالهای زمان-پیوسته مورد استفاده قرار میگیرد، به شکل زیر تعریف میشود:
در حالیکه جمع کانولوشن برای سیگنالهای زمان-گسسته استفاده میشود:
کانولوشن در مطالعه و استفاده از سیستمهای خطی تغییرناپذیر با زمان یا فیلترها همچون فیلترهای پایینگذر، میانگذر، میاننگذر و بالاگذر به شدت مورد توجه است و کاربرد دارد. یک سیستم زمان-پیوسته تغییر ناپذیر با زمان توسط تابع پاسخ ضربه خود مشخص میشود که معمولا به صورت نمایش داده میشود و برابر با خروجی سیستم به ازای ورودی برابر با تابع ضربه واحد است (تابع دلتا دیراک اعمال شده در زمان
). برای سیستمهای زمان-گسسته تغییرناپذیر با شیفت زمانی گسسته، تابع پاسخ ضربه خروجی سیستم به ازای ورودی ضربه زمان-گسسته است (تابع دلتا کرونکر – Kronecker Delta). برای سیستمهای زمان-پیوسته با ورودی دلخواه
، خروجی
و به طور معادل، برای سیستمهای زمان-گسسته تغییر ناپذیر با شیفت زمانی با ورودی دلخواه
، خروجی
با فرمولهای بالا داده میشوند.
کانولوشن معمولا برای دانشجویان جدید در مبحث پردازش سیگنال به لحاظ درک مفهومی و محاسبه روی کاغذ، کمی دشوار است و البته در صورت پیچیده بودن توابع و
میتواند برای هر کسی دشوار و سخت باشد. بنابراین در این نوشتار، چندین مثال ارائه خواهد شد که نحوه محاسبه کانولوشن بر روی کاغذ را در کنار محاسبه آن توسط نرمافزار متلب (MATLAB) نمایش میدهد.
پیشنهاد: فیلم آموزشی “کانولوشن و همبستگی در دنبالههای زمان-گسسته” را مشاهده کنید.
تئوری کانولوشن
یک قضیه کمکی مهم در محاسبه کانولوشن و همچنین در انواع مختلف تحلیلهای مربوط به سیستمهای خطی، تئوری کانولوشن است. این تئوری میگوید که تبدیل فوریه یک کانولوشن (یعنی تبدیل فوریه ) برابر است با حاصلضرب تبدیل فوریه سیگنالهایی که تحت عملیات کانولوشن قرار میگیرند. به زبان ریاضی، میتوان نوشت:
که نتیجه میدهد:
به طور مشابه، اگر کانولوشن در حوزه فرکانس داشته باشیم، تبدیل معکوس کانولوشن برابر است با حاصلضرب تبدیل معکوس فوریه توابعی که تحت کانولوشن قرار گرفتهاند:
که در آن
و
این نتایج به طور خلاصه چنین قابل بیان است: “کانولوشن در یک حوزه معادل با ضرب در حوزه دیگر است”.
مثال کانولوشن، محاسبه دستی
مثال متعارف برای کانولوشن معمولا کانولوشن یک مستطیل با خودش است. بنابراین این مثال را با جزییات و از دریچههای مختلف بررسی خواهیم کرد. در این نگاه اولیه، محاسبات لازم برای تعیین انتگرال کانولوشن انجام میشود.
ما میخواهیم یک مستطیل را با خودش کانوالو (convolve) کنیم. یک مستطیل با ارتفاع واحد و عرض واحد که معمولا تحت عنوان تابع
شناخته میشود:
تعریفهای جایگزین دیگری نیز برای وجود دارد که به شکلهای متفاوتی با مقادیر تابع در
رفتار میکنند. البته این موضوع برای ما چندان اهمیتی ندارد زیرا ما با توابعی که به شکل ساده انتگرالپذیر هستند سروکار داریم و حاصل کانولوشن آنها معمولا تابع پیوسته است.
یک مستطیل با ارتفاع و عرض
و مرکز
به سادگی بر حسب تابع
به شکل زیر قابل بیان است:
همانطور که در شکل 1 نشان داده شده است.
بنابراین سوال فعلی که پیش میآید این است: حاصل کانولوشن یا چیست؟ انتگرال کانولوشن در این حالت عبارت است از:
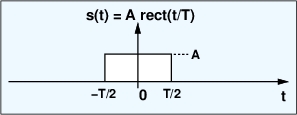
شکل 1- تابع مستطیلی با ارتفاع و عرض
که در مرکز
قرار گرفته است.
حال باید با توجه به فرمول انتگرال کانولوشن، عبارت زیر انتگرال کانولوشن یا برای هر مقدار
محاسبه شود. این بدان معنی است که باید تابع
را دقیق بشناسیم. تابع
نسخه معکوس زمانی
است و از آنجاییکه
نسبت به
متقارن است، میتوان نتیجه گرفت که
زیرا تابع مستطیلی ما نسبت به مرکز مختصات، متقارن است.
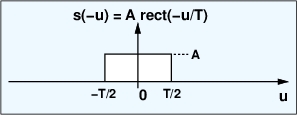
شکل 2- تابع مستطیلی متقارن با نمونه معکوس زمانی خود،
، یکسان است.
حضور متغیر در عبارت
مستطیل
را به اندازه
واحد زمانی شیفت میدهد. فرض کنید مقدار
بزرگ و منفی است. بنابراین مستطیل شیفت داده شده
به مرکز
خواهد بود که مقداری بزرگ و منفی است. به بیان دیگر، زمانیکه
مقدار قابل توجه و منفی باشد، مستطیل نمایش داده شده با عبارت
به مقدار قابل توجهی به سمت چپ محور
شیفت داده میشود. به طور مشابه، زمانیکه
مثبت باشد، مستطیل
به سمت راست شیفت داده میشود.
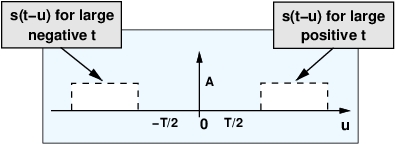
شکل 3- نمایش برای مقادیر
مثبت و منفی
روشی که ما برای محاسبه کانولوشن در پیش خواهیم گرفت، شروع از یک مقدار بزرگ و منفی و سپس افزایش آن تا زمانیکه مقداری بزرگ و مثبت شود، است. این فرآیند به این شکل قابل تصور است که ابتدا سیگنال مورد نظر را نسبت به مرکز خود بچرخانیم (معکوس زمانی)، به منتهیالیه سمت چپ منتقل کنیم (مقدار
بزرگ و منفی)، سپس سیگنال معکوس زمانی و شیفت داده شده را به سمت راست حرکت دهیم، مقادیر
را برای هر
محاسبه کنیم و با استفاده از آن انتگرال کانولوشن را برای هر مقدار
محاسبه کنیم. در ادامه مقاله و در بخش مثالهای ویدئویی، این موضوع توسط ویدئوهای خروجی متلب نشان داده شده است. اما فعلا ما تحلیل محاسبه دستی را پیش میبریم.
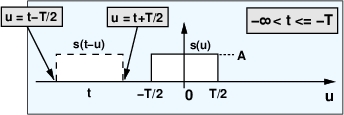
شکل 4- دو تابع در محاسبه کانولوشن – عبارتهای زیر انتگرال شامل و
، که برای
بزرگ و منفی همپوشانی نداشته باشند.
برای مستطیل معکوس زمانی و شیفت داده شده
همپوشانی با سیگنال
ندارد، بنابراین حاصضرب
صفر خواهد بود و بنابراین انتگرال کانولوشن نیز صفر است:
با ادامه حرکت به سمت راست با افزایش
در
لبه راست
مماس با لبه چپ
میشود. همچنان که
افزایش یافته و از
بیشتر میشود، دو مستطیل دچار همپوشانی میشوند. زمانیکه
در
ضرب میشود، تابع حاصل که تابعی از
است، تنها برای مقادیر
در ناحیه همپوشانی غیرصفر است.
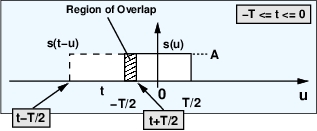
شکل 5- زمانیکه t از عبور میکند، مستطیلها شروع به همپوشانی میکنند. میزان همپوشانی در
کامل میشود. برای تمام مقادیر
لبه چپ و راست ناحیه همپوشانی به ترتیب در
و
قرار دارد.
مقدار انتگرال کانولوشن به نوعی مساحت زیر منحنی برای مقادیر ایی است که در ناحیه همپوشانی قرار میگیرند. برای
همپوشانی کامل میشود. در این حالت که ناحیه همپوشانی یک مستطیل ساده است، میتوانیم مقدار انتگرال را ذهنی محاسبه کنیم اما اجازه دهید برای تمرکز بهتر روی جزییات، آن را بنویسیم:
برای خواهیم داشت:
برای بررسی این نتیجه، توجه کنید که برای داریم:
که باید چنین باشد زیرا در این حالت ناحیه همپوشانی تنها یک نقطه است. برای
، مقدار
را داریم که خیلی ساده مساحت مستطیل
است زیرا در
دو مستطیل دقیقا روی هم قرار میگیرند.
پس از عبور از صفر، با افزایش ، لبه چپ
داخل
حرکت میکند و لبه راست آن از
عبور میکند و بنابراین همپوشانی بین دو مستطیل شروع به کاهش میکند. در
، ناحیه همپوشانی به یک نقطه تبدیل میشود و مجدد انتگرال کانولوشن صفر میشود:
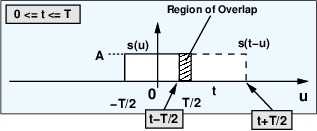
شکل 6- زمانیکه از صفر عبور میکند اما هنوز کمتر از
است، مستطیلها همپوشانی دارند ولی با افزایش
ناحیه همپوشانی کاهش مییابد.
در نهایت، زمانیکه است، دو مستطیل هیچ همپوشانی ندارند و انتگرال کانولوشن برای تمامی مقادیر
صفر خواهد بود:
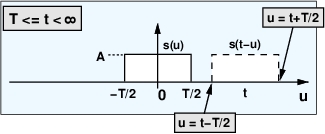
شکل 7- برای ، همپوشانی بین دو مستطیل یا یک نقطه تنها است
و یا اینکه تهی است
که در هر صورت انتگرال کانولوشن صفر میشود.
خلاصه نتایج بخشهای مختلف تاکنون برای بازههای زمانی متفاوت ، به شکل فرمول زیر است:
رسم نشان میدهد که حاصل کانولوشن یک تابع مثلثی با ارتفاع
و عرض
است، همانطور که در شکل زیر نشان داده شده است:
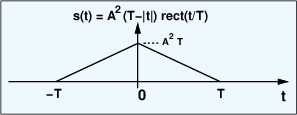
شکل 8- نتیجه کانولوشن یک مستطیل با ارتفاع و عرض
با خودش یک مثلث با ارتفاع
و عرض
است.
به طور مشابه میتوانید بررسی کنید که حاصل کانولوشن دو مستطیل با عرض یکسان و ارتفاعهای
به مثلثی با عرض
و ارتفاع
منجر میشود.
مثالهای از کانولوشن محاسبه شده با متلب
همانطور که در بخش قبل دیدیم، برخی از کانولوشنها به صورت مستقیم و با محاسبه دستی انتگرال کانولوشن (یا جمع در حالت زمان-گسسته) قابل محاسبه است. اما در بسیاری از حالتها این روش بسیار سخت یا غیرعملی خواهد بود و بنابراین بهتر است از روشهای عددی از طریق کدنویسی یا توابع آماده محاسبه کانولوشن که توسط بستههای نرمافزاری پیچیده همچون متلب یا پایتون(Python) فراهم شده است، استفاده شود. چنین نرمافزارهایی برای محاسبه حوزه زمان کانولوشن به طور مستقیم با کمک قضیه کانولوشن قابل استفاده است.
در اینجا تمرکز ما بر روی نرمافزار متلب است. البته با نوشتن کد محاسبه کانولوشن از پایه توسط خودتان چیزهای زیادی خواهید آموخت ولی فعلا نحوه استفاده از دستورهای استاندارد متلب برای انجام کانولوشنها را بررسی میکنیم. در طول این مسیر، مثالهای ارائه شده دید تکنیکی مناسبی در مورد اینکه کانولوشن چه کاری انجام میدهد و به چه معنی است، به شما خواهد داد.
ابزارهای اصلی متلب برای محاسبه کانولوشن توابع conv.m و filter.m هستند. برای استفاده از قضیه کانولوشن، ما به تبدیل فوریه نیاز داریم که تابع fft.m و تبدیل معکوس فوریه که ifft.m است. همچنین به ضرب برداری (سیگنالی) به صورت نقطهای نیز احتیاج هست. مثالهای پیش رو، در محاسبه مستقیم کانولوشن از conv.m استفاده میکنند اما به سادگی قابل تبدیل برای استفاده از filter.m هستند.
کانولوشن یک مستطیل با خودش
اجازه دهید مثال دستی که در ابتدای مقاله ذکر شد را مجدد بررسی کنیم، جاییکه یک سیگنال پالس مستطیلی با خودش کانوالو شد. در اینجا یک مستطیل به صورت یک بردار در متلب تولید میشود و سپس با استفاده از conv.m با خودش کانوالو میشود. عرض مستطیل 20 نمونه است و در شکل 9 نشان داده شده است. نتیجه استفاده از conv.m نیز در همان شکل 9 آمده است. از محاسبه دستی انجام شده در قبل، چنین انتظار داریم که حاصل کانولوشن، مثلثی با عرض نمونه و ارتفاع
باشد که همانطور که قابل مشاهده است، انتظارات تایید میشوند.
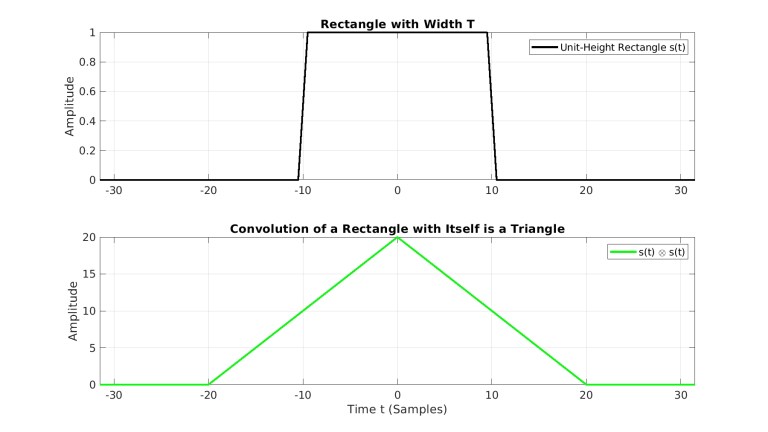
شکل 9- تابع conv.m متلب برای انجام کانولوشن یک بردار شامل سیگنال پالس مستطیلی با خودش استفاده شده است. نتیجه همان تابع مثلثی مورد انتظار است.
کانولوشن یک مستطیل دوبار با خودش
در ادامه از conv.m برای کانولوشن یک مستطیل با خودش و مجدد کانولوشن نتیجه مرحله قبل با همان مستطیل استفاده میشود. به عبارت دیگر، اگر مستطیل را با نمایش دهیم، ما در تلاش برای محاسبه
هستیم. نتیجه در شکل 10 نمایش داده شده است. دقت کنید که نتیجه کانولوشن هر بار عریضتر میشود و بنابراین
دو برابر عریضتر از
و
نیز به اندازه عرض
عریضتر از
است. یک خاصیت اصلی کانولوشن با یک سیگنال پالس-مانند همچون
این است که: خروجی کانولوشن هموارتر و صافتر از ورودی است. در حالیکه ورودی
شامل دو ناپیوستگی به شکل تابع پله است و به نوعی تابع هموار به حساب نمیآید،
پیوسته است اما در مشتق خود ناپیوستگی دارد (در
). تابع
همانطور که به لحاظ ظاهری مشهود است، پیوسته بوده و مشتق اول پیوسته نیز دارد. خروجیهای کانولوشن نسبت به ورودی آن هموارتر (دارای ناپیوستگیهای کمتر) هستند. بنابراین، برخی اوقات کانولوشن با یک تابع پالس-مانند (مثلا یک مستطیل) تحت عنوان فرآیند هموارسازی (smoothing) نیز شناخته میشود.
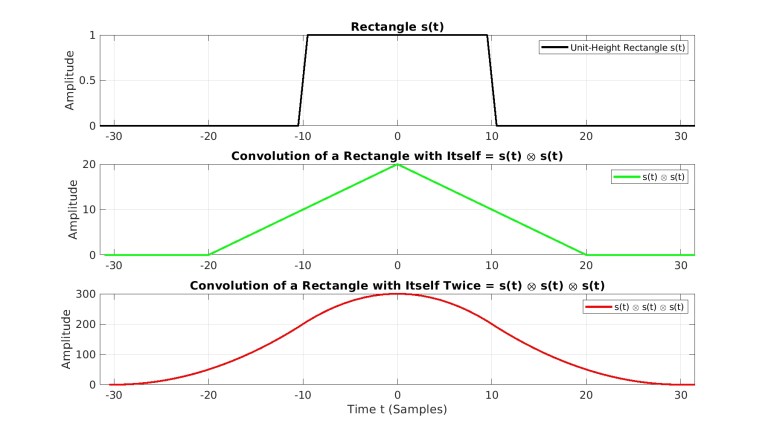
شکل 10- یک مستطیل، حاصل کانولوشن با خودش و کانولوشن با خودش دو مرتبه. توابع حاصل هموارتر میشوند همچنان که به لحاظ زمانی نیز عریضتر میشوند.
کانولوشن یک مثلث با خودش
حال اجازه دهید کانولوشن دشوارتری را به دو شکل انجام دهیم. راه اول استفاده از conv.m و راه دوم استفاده از قضیه کانولوشن است. سیگنال به شکل یک مثلث است که در شکل 10 نشان داده شده است، که خود حاصل کانولوشن مستطیل s(t) با خودش است. ما میخواهیم کانولوشن مثلث را با خودش محاسبه کنیم. به سادگی میتوان تابع conv.m را برای دستیابی به شکل 11 اعمال کرد. دقت کنید که این تابع مشابه بخش پایینی شکل 10 است که در آن کانولوشن یک مستطیل دو بار با خودش محاسبه شده است اما هنوز کمی هموارتر به نظر میرسد زیرا در شکل 11 در واقع کانولوشن مستطیل با خودش به تعداد چهار مرتبه انجام شده است یا کانولوشن یک مثلث با خودش دو بار در حالیکه بخش پایینی شکل 10 کانولوشن مستطیل سه بار با خودش انجام شده است.
تئوری کانولوشن میگوید که ما میتوانیم کانولوشن یک مثلث با خودش را به کمک تبدیل فوریه مثلث، ضرب این تبدیل به صورت نقطهای با خودش و در نهایت محاسبه تبدیل معکوس فوریه حاصلضرب بدست آوریم. تبدیل فوریه مثلث در بخش میانی شکل 11 نشان داده شده است و خروجی روش مبتنی بر تئوری کانولوشن بخش پایینی شکل 11 است. مشاهده میکنیم که بخشهای بالایی و پایینی شکل یکسان هستند همانطور که انتظار داریم.
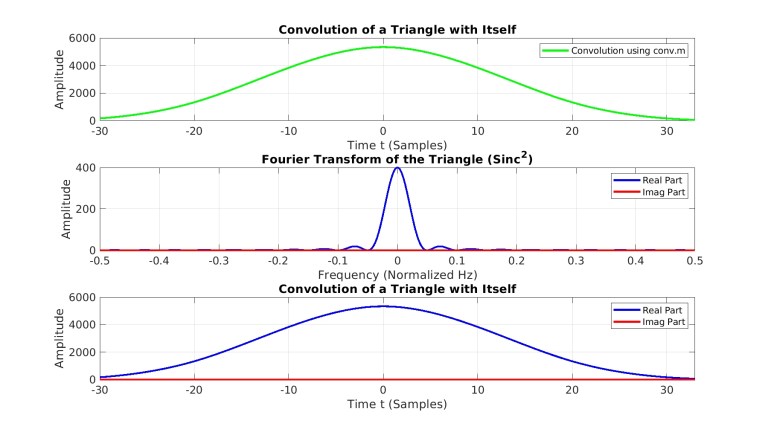
شکل 11- کانولوشن مثلث شکل 10 با خودش به دو روش: کانولوشن مستقیم با استفاده از conv.m در متلب و کانولوشن غیرمستقیم از طریق قضیه کانولوشن، با استفاده از تابع fft.m،
ifft.m و ضرب برداری عضو محور (نقطهای)
کانولوشن قطار ضربه مدوله شده با توابع شکل دهنده پالس مختلف
در مثالهای پیش رو امید آن است که دید شما نسبت به تاثیرگذاری و عملکرد کانولوشن در مفاهیم مربوط به مخابرات فرکانس رادیویی (RF) تقویت شود. در این بخش تمرکز ما بر روی کانولوشن یک قطار پالس مدوله شده با توابع پالس-مانند مختلف است که در عمل مدل مناسبی برای تولید سیگنال مخابراتی RF است.
یک قطار ضربه مدوله شده مجموعهای از پالسها (توابع دلتا کرونکر) است که به میزان ثابتی در زمان، مثلا T، از هم جدا شدهاند و هر کدام با مقدار تصادفی تحت عنوان سمبل (symbol) ضرب شدهاند. در اینجا سمبلها را به مجموعه مقادیر باینری محدود میکنیم. یک قطار ضربه مدوله شده نوعی با ثابت جداسازی زمان
در بخش بالایی شکل 12 نشان داده شده است.
بخش میانی شکل 12 قطار ضربه مدوله شده را پس از کانوالو کردن آن با پالس مستطیلی با عرضی بسیار کمتر از نشان میدهد. معکوس زمانی این مستطیل و شیفت آن به سمت نقطه منفی بینهایت را تصور کنید و سپس حرکت آن در طول محور زمانی به سمت راست را در نظر بگیرید. در هر لحظه زمانی، پالس و قطار ضربه را در هم ضرب کنید و مساحت زیر منحنی حاصل را محاسبه کنید. خواهید دید که چیزی که در حال اتفاق افتادن است تکرار پالس مستطیلی باریک در مکان هر ضربه از قطار ضربه مدوله شده است ولی در هر تکرار با اندازه تصادفی در ضربهها ضرب میشود و این دقیقا همان چیزی است که در بخش میانی شکل 12 دیده میشود. بخش پایین این شکل، فرآیند مشابهی را نشان میدهد ولی در آن عرض پالس مستطیلی برابر با میزان جدایی هر ضربه،
، است و بنابراین هیچ فضای خالی بین پالسهای تکرار شده وجود ندارد. به این ترتیب، ما میتوانیم سیگنال مدولاسیون اندازه پالس (Pulse Amplitude Modulation-PAM) را به کمک هر تابع پالس-مانند دلخواه و کانولوشن آن با قطار ضربه مدوله شده تولید کنیم. اگر ما سیگنال بخش پایینی شکل 12 را در موج سینوسی با مقادیر مختلط ضرب کنیم، سیگنال پالس مستطیلی مدولاسیون BPSK بوجود میآید.
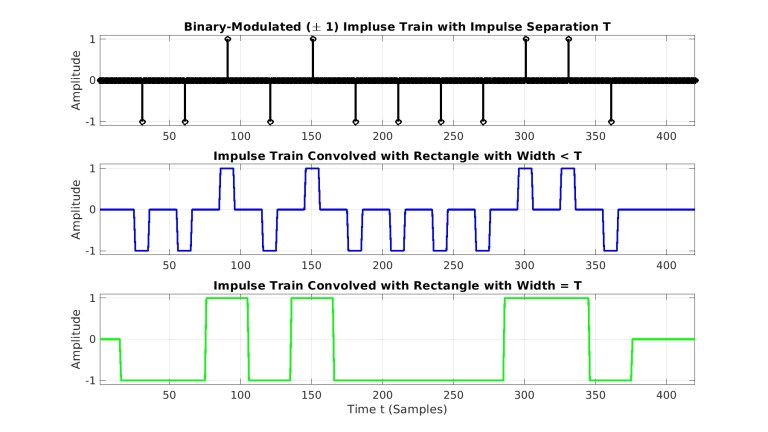
شکل 12- قطار ضربه مدوله شده باینری (بالا)، کانولوشن قطار ضربه مدوله شده باینری با پالس مستطیلی باریک (وسط)، کانولوشن قطار ضربه مدوله شده باینری با پالس مستطیلی که عرض آن برابر با فاصله پالسها در قطار ضربه است.
در شکل 13 حالتهای مختلفی از آزمایش انجام شده در شکل 12 نشان داده شده است که در آن پالسهای مستطیلی با توابع سینوسی نیم-تناوب جایگزین شدهاند. بخش میانی این شکل حالت نیم-کسینوسی باریک (نسبت به ) را نشان میدهد و بخش پایینی حالتی را که عرض نیم-تناوب برابر با میزان جدایی ضربهها از یکدیگر است. بخش پایینی دقیقا همان چیزی است که سیگنال مدولاسیون کلیدزنی حداقل شیفت (Minium Shift Keying – MSK) به عنوان بخش همفاز(In-phase) خود از آن استفاده میکند. این روش از نسخه تاخیر یافته همین سیگنال با سبملهای مستقل برای بخش تربیعی (Quadrature) بهره میبرد. مقدار تاخیر، نصف دوره تناوب سمبل،
، است همچنان که در تمامی سیگنالهای مدولاسیون کلیدزنی شیفت فاز آفست (OQPSK) همچون OQPSK,MSK,GMSK نیز چنین است.
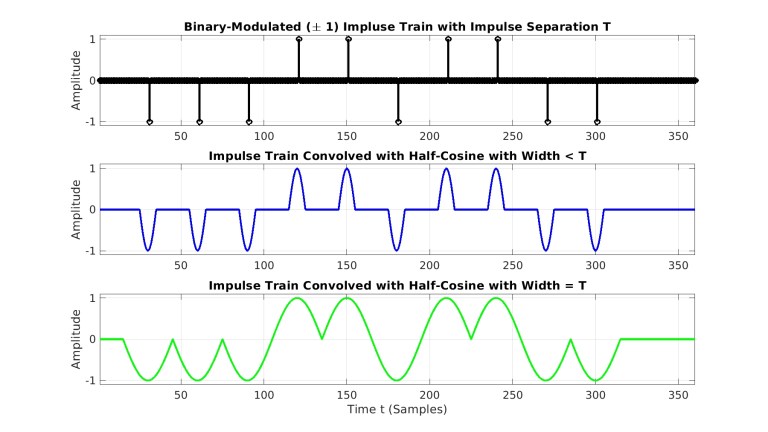
شکل 13- قطار ضربه مدوله شده باینری (بالا)، کانولوشن قطار ضربه باینری مدوله شده با پالس نیم-تناوب باریک کسینوسی (وسط)، کانولوشن قطار ضربه باینری مدوله شده با پالس نیم-تناوب کسینوسی با عرض برابر با میزان جدایی بین ضربهها در قطار پالس (پایین).
در نهایت، در شکل 14 آزمون قطار ضربه با یک پالس کاربردی مهم تکرار میشود: پالس کسینوسی ارتقا یافته ریشه دوم (Square root raised cosine – SRRC). با استفاده از همان روشهای به کار رفته برای شکلهای 11 و 12، دو حالت را بررسی میکنیم: حالت باریک در زمان برای پالس SRRC (بخش میانی) و پالس SRRC طراحی شده برای نرخ سمبل برگرفته از میزان جدایی ضربهها از هم در شکل بالایی. سیگنال پایینی مدل مناسبی برای سیگنال BPSK بدون نویز و کاهش فرکانس یافته است که از پالسهای SRRC استفاده میکند.
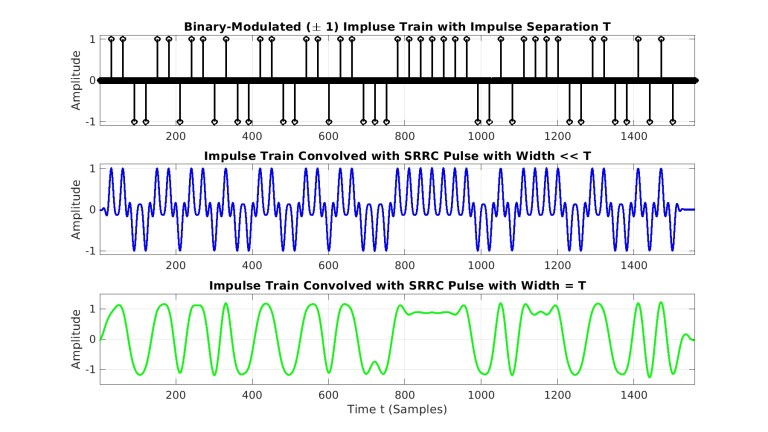
شکل 14- قطار ضربه مدوله شده باینری (بالا)، کانولوشن قطار ضربه مدوله شده باینری با پالس SRRC باریک (وسط)، کانولوشن قطار ضربه مدوله شده باینری با پالس SRRC طراحی شده برای شکل دهی قطار پالس با میزان جدایی (پایین).
مثال کانولوشن با ویدئو
در این بخش چندین ویدئو نمایش داده میشود که عملکرد کانولوشن را بهتر نشان میدهد. هر فریم از یک ویدئو دو تابع زیر انتگرال کانولوشن، حاصلضرب آنها و نتیجه خود انتگرال را نشان میدهد. به عبارت دیگر، اگر کانولوشن بین و
به شکل زیر داده شده باشد:
ما سیگنالهای را در محورهای مجزا نشان میدهیم. هر فریم ویدئو متناظر با یک مقدار متفاوت
است. به عبارتی این ویدئوها فرآیند معکوس زمانی-حرکت یا لغزش توابع نسبت به هم – انتگرال گیری را که در کانولوشن نهفته است، نشان میدهند.
ویدئو اول مربوط به کانولوشن مستطیل با ارتفاع واحد و عرض 40 یا با مستطیل دیگری به فرم
که ارتفاع 2 و عرض 40 دارد، است. با توجه به مطالب قبل، میدانیم که نتیجه کانولوشن یک مثلث با عرض
و ارتفاع
خواهد بود.
ویدئو 1- کانولوشن دو مستطیل با عرضهای 40 و ارتفاعهای متفاوت.
در ویدئو دوم ما کانولوشن دو مثلث با عرض 40 نمونه و ارتفاعهای متفاوت را محاسبه میکنیم.
ویدئو 2- نمایش گام به گام کانولوشن دو مثلث با عرض یکسان و ارتفاع متفاوت
در نهایت در ویدئو سوم، ما اثر فرآیند هموارسازی یک موج سینوسی نویزی را بررسی کرده و نمایش میدهیم. موج سینوسی نویزی با مستطیل با مساحت واحد کانوالو میشود. عرض مستطیل کمتر از نصف تناوب موج سینوسی است. همانطور که از نتیجه کانولوشن، ، قابل ملاحظه است، اثر کانولوشن حذف بخشی از نویز دیده شده در موج سینوسی است که در شکل به وضوح مشخص است. این فرآیند کانولوشن همچنین به نوعی یک فیلتر پایینگذر است زیرا اگر مستطیل را به شکل پاسخ ضربه یک سیستم خطی تغییرناپذیر با زمان (
) در نظر بگیریم، تابع تبدیل متناظر یک تابع سینک به مرکز مبداء مختصات محور فرکانس خواهد بود. تنها اجزاء فرکانسی که درون لوب اصلی تابع سینک قرار گرفتهاند با دامنه کافی از سیستم خطی عبور میکنند، در نتیجه اجزاء نویز که خارج از لوب اصلی قرار گرفتهاند تضعیف میشوند.
ویدئو 3- کانولوشن مستطیل با مساحت واحد با موج سینوسی نویزی. خروجی کانولوشن، ، میتواند به عنوان خروجی سیستم خطی تغییرناپذیر با زمانی فرض شود که ورودی این سیستم موج سینوسی نویزی و پاسخ ضربه این سیستم مستطیل با مساحت واحد است. چنین فرآیندی فیلتر پایینگذر و یا فیلتر میانگین متحرک (moving average) نیز میتواند نام بگیرد.
یک نتیجه عجیب و جالب از قضیه کانولوشن
اجازه دهید مجدد تابع مستطیلی با ارتفاع واحد و عرض را در نظر بگیریم که تحت عنوان
شناخته میشود. از قبل میدانیم که تبدیل فوریه پالس مستطیلی یک تابع سینک است:
همچنان که در شکل 16 نشان داده شده است. از آنجاییکه مستطیلی ارتفاع واحد دارد، زمانیکه آن را در خودش ضرب کنیم این ارتفاع تغییری نمیکند:
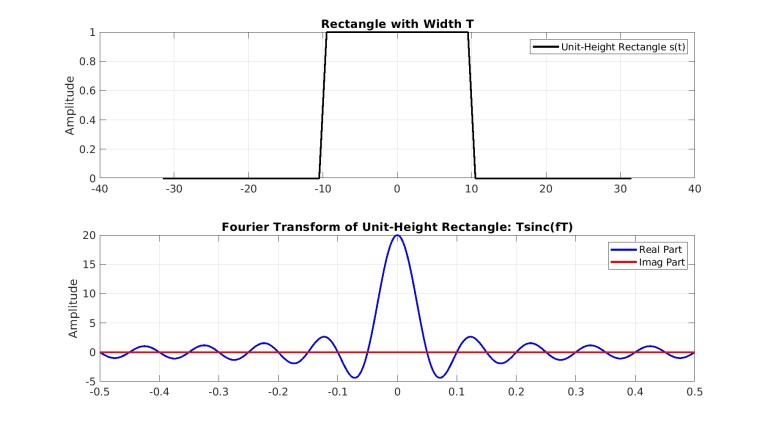
شکل 16- تابع مستطیلی با عرض و تبدیل فوریه آن، تابع سینک.
از این موضوع به سرعت میتوان چنین نتیجهگیری کرد که تبدیل فوریه مربع تابع مستطیلی با ارتفاع واحد نیز یک تابع سینک خواهد بود:
اما طبق قضیه کانولوشن، تبدیل فوریه حاصلضرب دو مستطیل برابر است با کانولوشن تبدیل فوریه آنها:
در نتیجه تابع سینک تحت کانولوشن نامتغیر است. به عبارت دیگر کانولوشن یک سینک با سینک دیگر خود یک تابع سینک است:
از آنجاییکه کانولوشن
تابع سینک با هم نیز همان تابع سینک اصلی میشود. در شکل 17، تبدیل فوریه تابع
و همچنین کانولوشن آن با خودش رسم شده است که برابری آنها را با یکدیگر نشان میدهد.
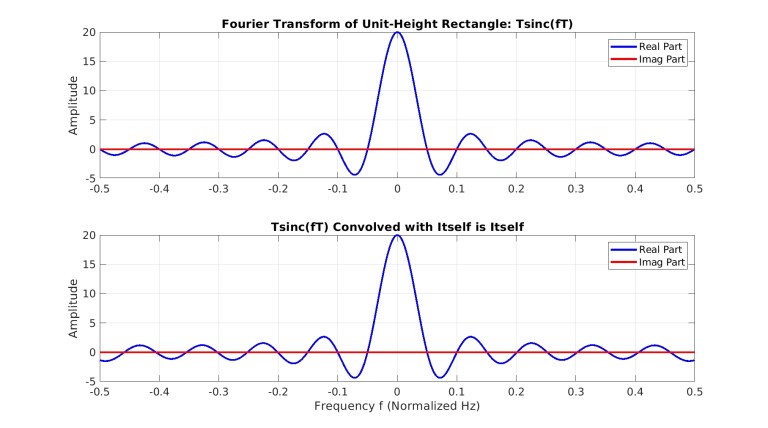
شکل 17- تبدیل فوریه مستطیل با ارتفاع واحد (بالا) و کانولوشن آن با خودش (پایین)
این مساله یک نتیجه مهم دیگر دارد که همان برابری نتیجه کانولوشن تابع سینک به تعداد N بار با خودش با همان تابع اولیه است:
ویدئو زیر تابع سینک را که با خودش کانوالو میشود، نشان میدهد:
ویدئو 4- نمایش کانولوشن یک تابع سینک با خودش
میتوان چنین تصور کرد که برخی سیگنالهای دیگر با چنین خاصیتی وجود داشته باشند.
منبع: https://cyclostationary.blog/2021/01/28/sptk-convolution-and-the-convolution-theorem/#more-6445

دیدگاه ها (3)
با عرض سلام و خسته نباشید خدمتتون خیلی تشکر میکنم بابت مقاله خوبتون واقعا خیلی کمکم کرد این بحث از هیچ منبع دیگه ای انقدر کامل و واضح توضیحشو پیدا نکرده بودم فقط یک سوال
در شکل یازده که تابع مثلث با خودش convolve شده چرا عرض مثلث برابره با زمانی که تابع مستطیل ۳ بار با خودش convolve شده؟ مگه نباید تو شکل یازده عرض برابر 4T مستطیل یعنی از 40- تا 40+ بشه؟
ممنون از توجه و لطف شما. در شکل یازده عرض حاصل کانولوشن 40- تا 40+ است ولی چون مقادیر کم هستند در شکل نشان داده نشده است. اگر دقت کنید بعد از 30+ و قبل از 30- هنوز منحنی بالای محور x است که نشان میدهد هنوز حاصل کانولوشن غیرصفر است.
خیلیم عالی
مرسی بابت پاسخگویی🙏