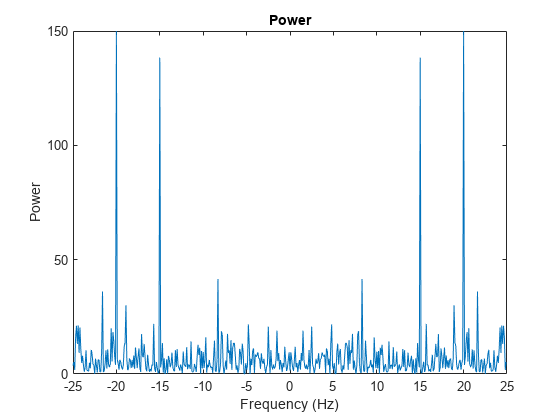
نمودار تبدیل فوریه سریع (FFT) موج سینوسی در متلب

 

 

 

نمودار تبدیل فوریه سریع (FFT) موج سینوسی در متلب (MATLAB)

 

 

 

در این مقاله، هدف یادگیری نحوه رسم تبدیل فوریه سریع یا FFT موج سینوسی با استفاده از نرم‌افزار متلب است. مفاهیمی همچون fftshift، طیف یکطرفه، طیف دوطرفه و طیف نرمالیزه شده نیز مطرح میشوند.

 

 

مقدمه

 

متون متعددی درباره اصول تبدیل فوریه گسسته (DFT) و پیاده‌سازی بسیار کارآمد آن، FFT، در دسترس است. اغلب با نیاز به تولید سیگنالهای استاندارد همچون سیگنال سینوسی، کسینوسی، پالس گوسین، موج مربعی، موج مستطیلی جدا از هم، نمایی میرا و سیگنال چهچه یا chirp برای اهداف شبیه‌سازی مواجه میشویم. هدف این مقاله، بررسی نحوه تولید سیگنال سینوسی در متلب و  نمایش آن در حوزه فرکانس با استفاده از FFT است.

 

 

موج سینوسی

 

برای تولید موج سینوسی، اولین گام، مشخص کردن فرکانس موج است. برای مثال، در اینجا میخواهیم موج سینوسی با تولید کنیم که حداکثر و حداقل اندازه دامنه آن به ترتیب 1+ و 1- است. حال که فرکانس موج مشخص شده است، گام بعدی تعیین نرخ نمونه‌برداری است که با توجه به شرایط شبیه‌سازی در متلب انجام میشود.

 

 

پیاده‌سازی در متلب

 

نرم‌افزار متلب هر چیزی به فرم دیجیتال را میتواند پردازش کند. برای تولید و رسم موج سینوسی هموار، نرخ نمونه‌برداری باید خیلی بالاتر از میزان تعیین شده حداقلی توسط قضیه شانون-نایکوئیست (Nyquist Shannon Theorem) که حداقل دو برابر فرکانس ماکزیمم موجود در سیگنال است، باشد. فاکتور بیش‌نمونه‌برداری (oversampling) در اینجا برابر با 30 در نظر گرفته میشود (این مقدار بالا بدین منظور انتخاب میشود که موج سینوسی به ظاهر پیوسته تولید شود). بنابراین نرخ نمونه‌برداری برای شبیه‌سازی در متلب، برابر با انتخاب میشود. اگر شیفت فاز نیز برای این کار نیاز دارید، میتوانید مقداری برای آن در نظر بگیرید.

 

f=10; %frequency of sine wave

overSampRate=30; %oversampling rate

fs=overSampRate*f; %sampling frequency

phase = 1/3*pi; %desired phase shift in radians

nCyl = 5; %to generate five cycles of sine wave

t=0:1/fs:nCyl*1/f; %time base

x=sin(2*pi*f*t+phase); %replace with cos if a cosine wave is desired

plot(t,x);

title([‘Sine Wave f=’, num2str(f), ‘Hz’]);

xlabel(‘Time(s)’);

ylabel(‘Amplitude’);

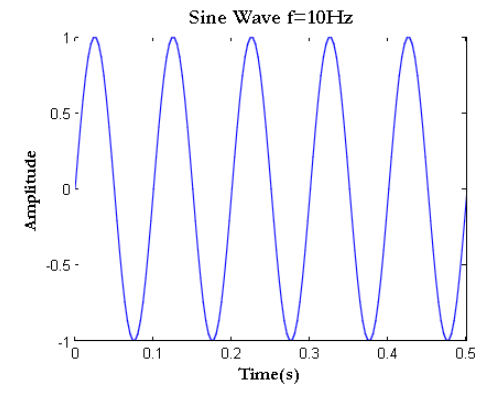
شکل 1- موج سینوسی با فرکانس 10 هرتز در متلب

 

 

نمایش حوزه فرکانس

 

نمایش سیگنال داده شده در حوزه فرکانس از طریق تبدیل فوریه سریع FFT انجام میشود. معمولا، طیف توان برای تحلیل در حوزه فرکانس استفاده میشود. در طیف توان، توان هر جزء فرکانس از سیگنال مورد نظر، بر حسب فرکانس رسم میشود. دستور fft(x,N) در متلب، تبدیل  N-نقطه‌ای DFT را محاسبه میکند. تعداد نقاط، N، در محاسبه DFT به صورت توانی از 2 در نظر گرفته میشود زیرا این کار به محاسبه کارآمدتر و بهتر در الگوریتم FFT کمک میکند. مقدار N=1024 در اینجا انتخاب شده است. همچنین میتوان مقدار آن را توانی از 2 در نظر گرفت که درست بعد از مقدار عددی طول سیگنال می‌آید.

 

 

نمایشهای مختلف از FFT

 

از آنجاییکه FFT یک نسخه محاسبه عددی شده از تبدیل N-نقطه‌ای DFT است، راههای مختلفی برای رسم نتیجه آن وجود دارد.

 

 

1- رسم مقادیر خام DFT

 

محور x از 0 تا N-1 شامل مقادیر نمونه‌های N-تایی است. از آنجاییکه مقادیر DFT مختلط هستند، در اینجا اندازه دامنه DFT یا abs(X) بر روی محور y رسم میشود. از این نمودار، فرکانس سیگنال سینوسی تولید شده قابل تشخیص نیست.

 

NFFT=1024; %NFFT-point DFT

X=fft(x,NFFT); %compute DFT using FFT

nVals=0:NFFT-1; %DFT Sample points

plot(nVals,abs(X));

title(‘Double Sided FFT – without FFTShift’);

xlabel(‘Sample points (N-point DFT)’)

ylabel(‘DFT Values’);

 

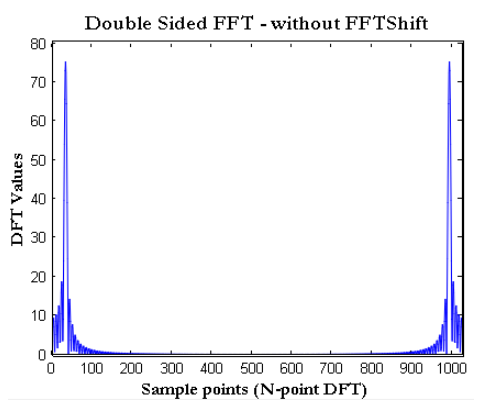
شکل 2- تبدیل فوریه سیگنال سینوسی

 

 

2- نمودار FFT – رسم مقادیر خام بر حسب محور فرکانسی نرمالیزه شده

 

در نسخه بعدی نمودار تبدیل فوریه، محور فرکانس (محور x)، به مقدار واحد نرمالیزه میشود. کافی است که اندیس نمونه بر روی محور x بر N، طول FFT، تقسیم شود. این کار، محور x را نسبت به فرکانس نمونه‌برداری نرمالیزه میکند. البته همچنان فرکانس موج سینوسی تولید شده از نمودار قابل فهم نیست.

 

NFFT=1024; %NFFT-point DFT

X=fft(x,NFFT); %compute DFT using FFT

nVals=(0:NFFT-1)/NFFT; %Normalized DFT Sample points

plot(nVals,abs(X));

title(‘Double Sided FFT – without FFTShift’);

xlabel(‘Normalized Frequency’)

ylabel(‘DFT Values’);

 

 

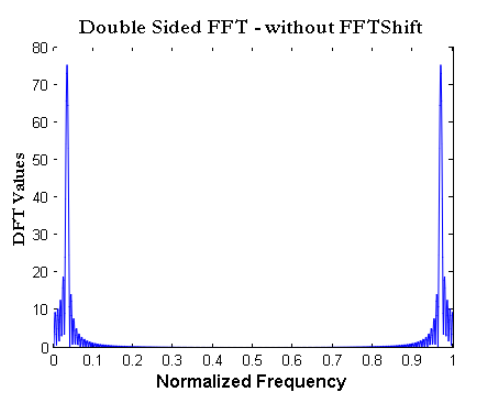
شکل 3- تبدیل فوریه سیگنال سینوسی بر روی محور فرکانس نرمالیزه

 

 

3- نمودار FFT – رسم مقادیر خام بر حسب فرکانس نرمالیزه در راستای فرکانسهای مثبت و منفی

 

همانطور که میدانید، در حوزه فرکانس، در هر دو بخش مثبت و منفی محور فرکانس، مقدار داریم. برای رسم مقادیر DFT بر روی محور فرکانس در هر دو بخش مثبت و منفی، مقدار DFT در اندیس نمونه صفر باید در مرکز آرایه قرار گیرد. این کار از طریق دستور fftshift در متلب انجام میشود. محور x از 0.5- تا 0.5+ است که در آن نقاط انتهایی در واقع فرکانسهای تاشده (folding frequencies) نسبت به نرخ نمونه‌برداری  است.

 

NFFT=1024; %NFFT-point DFT

X=fftshift(fft(x,NFFT)); %compute DFT using FFT

fVals=(-NFFT/2:NFFT/2-1)/NFFT; %DFT Sample points

plot(fVals,abs(X));

title(‘Double Sided FFT – with FFTShift’);

xlabel(‘Normalized Frequency’)

ylabel(‘DFT Values’);

 

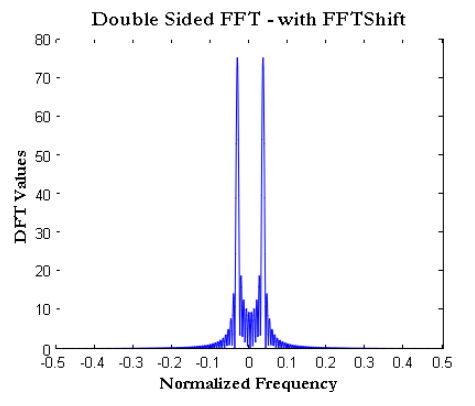
شکل 4- تبدیل فوریه سیگنال سینوسی بر روی محور فرکانسی نرمالیزه و به صورت دو طرفه

 

 

4- نمودار FFT –فرکانس مطلق بر روی محور x و اندازه طیف بر روی محور y

 

در اینجا، محور فرکانس نرمالیزه در نرخ نمونه‌برداری ضرب میشود. از نمودار بدست آمده کاملا واضح است که اندازه FFT بر روی فرکانسهای 10+ و 10- به حداکثر مقدار خود میرسد. بنابراین فرکانس موج سینوسی تولید شده 10 هرتز است. لوبهای فرعی کوچک در اطراف قله‌های نمودار حول فرکانسهای 10+ و 10- به دلیل نشت طیفی (spectral leakage) است.

 

NFFT=1024;

X=fftshift(fft(x,NFFT));

fVals=fs*(-NFFT/2:NFFT/2-1)/NFFT;

plot(fVals,abs(X),‘b’);

title(‘Double Sided FFT – with FFTShift’);

xlabel(‘Frequency (Hz)’)

ylabel(‘|DFT Values|’);

 

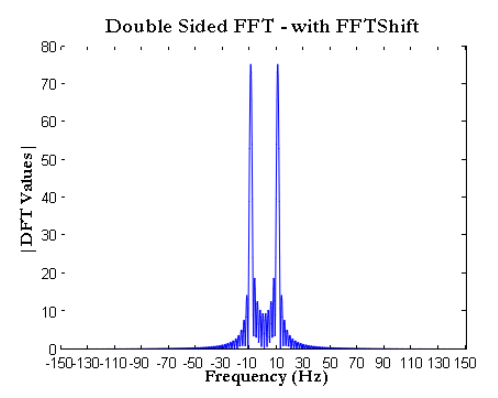
شکل 5- تبدیل فوریه سیگنال سینوسی بر روی محور فرکانسی مطلق و به صورت دو طرفه

 

 

5- طیف توان –فرکانس مطلق بر روی محور x و توان بر روی محور y

 

آنچه در ادامه می‌آید مهمترین نمایش FFT است. این نمودار، توان هر جزء فرکانسی بر روی محور y را به ازای هر فرکانس روی محور x رسم میکند. نمودار توان، قابل رسم بر روی مقیاس خطی یا لگاریتمی است. توان هر جزء فرکانس به شکل زیر محاسبه میشود:

 

 

که نمایش حوزه فرکانس است. در متلب، توان باید با مقیاس درست محاسبه شود زیرا ممکن است که طول سیگنال و تبدیل FFT آن یکسان نباشند.

 

NFFT=1024;

L=length(x);

X=fftshift(fft(x,NFFT));

Px=X.*conj(X)/(NFFT*L); %Power of each freq components

fVals=fs*(-NFFT/2:NFFT/2-1)/NFFT;

plot(fVals,Px,‘b’);

title(‘Power Spectral Density’);

xlabel(‘Frequency (Hz)’)

ylabel(‘Power’);

 

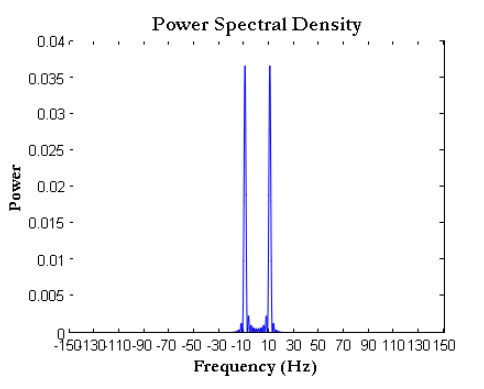
شکل 6- توان طیف سیگنال سینوسی بر روی محور فرکانسی مطلق و به صورت دو طرفه

 

 

رسم چگالی طیف توان (Power Spectral Density – PSD) بر روی محور لگاریتمی y، رایج‌ترین نوع نمودار PSD در پردازش سیگنال است.

 

NFFT=1024;

L=length(x);

X=fftshift(fft(x,NFFT));

Px=X.*conj(X)/(NFFT*L); %Power of each freq components

fVals=fs*(-NFFT/2:NFFT/2-1)/NFFT;

plot(fVals,10*log10(Px),‘b’);

title(‘Power Spectral Density’);

xlabel(‘Frequency (Hz)’)

ylabel(‘Power’);

 

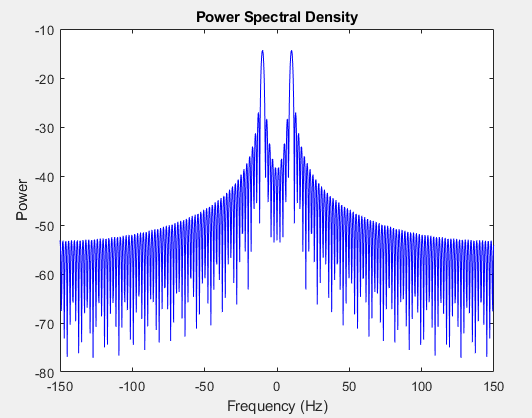
شکل 7- توان طیف سیگنال سینوسی بر روی محور فرکانسی مطلق و به صورت دو طرفه

 

 

6- طیف توان – طیف توان یکطرفه

 

در این نوع از نمودار، بخش منفی محور x حذف میشود. فقط مقادیر FFT متناظر با نمونه‌های 0 تا N/2 از تبدیل N-نقطه‌ای DFT، رسم میشوند. به طور معادل، محور فرکانس نرمالیزه نیز بین 0 تا 0.5 خواهد بود. فرکانس مطلق نیز از 0 تا است.

 

L=length(x);

NFFT=1024;

X=fft(x,NFFT);

Px=X.*conj(X)/(NFFT*L); %Power of each freq components

fVals=fs*(0:NFFT/2-1)/NFFT;

plot(fVals,Px(1:NFFT/2),‘b’,‘LineSmoothing’,‘on’,‘LineWidth’,1);

title(‘One Sided Power Spectral Density’);

xlabel(‘Frequency (Hz)’)

ylabel(‘PSD’);

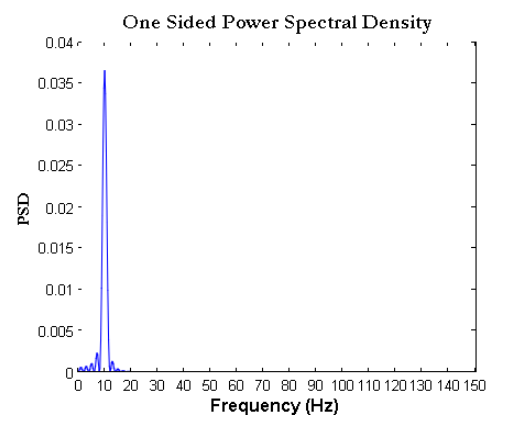
شکل 8- چگالی طیف توان یکطرفه سیگنال سینوسی بر روی محور فرکانسی مطلق و به صورت دو طرفه

 

 

 

 

 

منبع: www.gaussianwaves.com