معیارهای آماری در سیگنالهای تصادفی
تمرکز اصلی در این مقاله بحث در مورد معیارهای آماری مورد استفاده در سیگنالهای تصادفی همچون میانگین، واریانس، چولگی (skewness)، کشیدگی (kurtosis)، هیستوگرام، نمودار پراکندگی (scatter plot)، همبستگی متقابل (cross-correlation) و خود همبستگی (auto-correlation) است.
سیگنالهای قطعی و تصادفی
یک سیگنال قطعی برای یک بازه زمانی مشخص کامل و به طور دقیق قابل پیشبینی است. چنین سیگنالی میتواند به شکل رابطه آنالیز ریاضی (مثلا: ) بیان شود.
بسیاری از سیگنالهایی که در دنیای واقعی کاربردهای پردازش سیگنال با آنها مواجه میشویم، توسط معادلات آنالیزی قابل بیان و یا پیشبینی نیستند، زیرا آنها بخش نامطمئن و غیرقطعی خاصی در ارتباط با خود دارند. در نتیجه، چنین سیگنالهایی باید توسط مفاهیم آماری توصیف شوند. بنابراین، این گونه سیگنالها خارج از قلمرو سیگنالهای قطعی هستند و تحت عنوان سیگنالهای تصادفی کلاسبندی میشوند.
به طور مثال، فرض کنید که یک مدار الکتریکی را در اختیار داریم و ولتاژ دو سر یک مقاومت را برای یک تناوب زمانی مشاهده میکنیم. برپایه نظریه میدان الکتریکی، ذرات اتمی درون مقاومت تمایل به حرکت تصادفی دارند که به شکل حرارت خود را نشان میدهد. این حرکت بر پایه حرارت و به شکل تصادفی، منجر به نوسانهای تصادفی در ولتاژ اندازهگیری شده در دو سر مقاومت میشود. بنابراین، ولتاژ اندازهگیری شده میتواند از طریق توزیع احتمال مقادیر ولتاژ توصیف شود و بوسیله روشهای آماری مورد تجزیه و تحلیل قرار گیرد، اما با دقت بالا قابل پیشبینی نیست. این مورد مثالی است از یک سیگنال که تابعی تصادفی از زمان است. چنین توابعی معمولا برپایه قوانین احتمالات مشخص، تغییر و تکامل مییابند و فرض بر این است که توسط فرآیند تصادفی مربوط به خود تولید میشوند (حرکت بر پایه حرارت در مثال بالا).
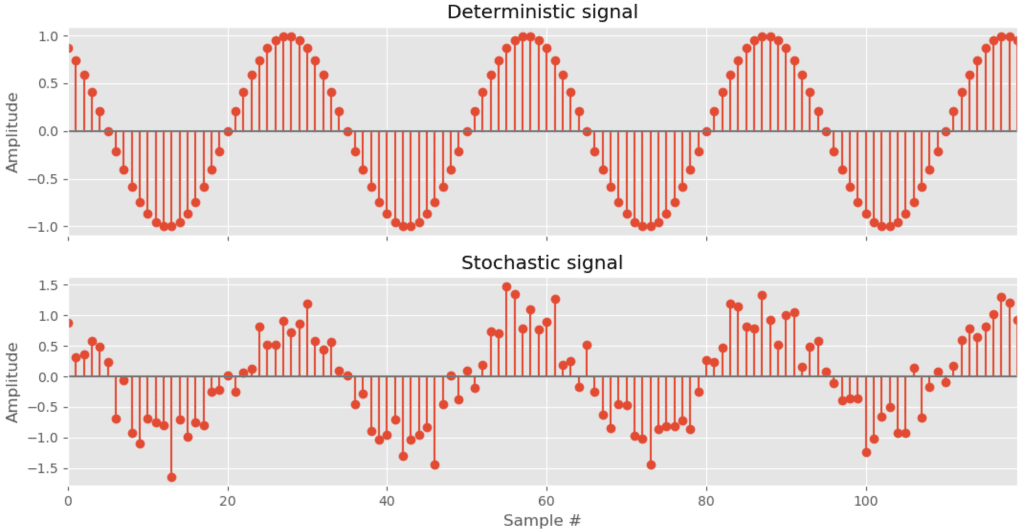
شکل 1- مثالهایی از سیگنال قطعی و تصادفی
با فرض داشتن اندازه سیگنال ولتاژ تصادفی در زمان ، حال میدانیم که نمیتوان مقدار آن را در زمان
پیشبینی کرد. هر چند که، اگر سیگنال را برای مدت زمان کافی تحت نظر بگیریم، میتوانیم به طور تجربی توزیع احتمال آن را بر اساس توانایی پاسخ به سوالهایی مشابه موارد زیر مشخص کنیم:
با داشتن اندازه ولتاژ در زمان ، مقدار میانگین ولتاژ در زمان
چقدر است؟
به چه میزان انتظار داریم که ولتاژ در زمان از مقدار متوسط خود کمتر یا بیشتر شود؟ به عبارت دیگر، میزان واریانس ولتاژ در زمان
چقدر خواهد بود؟
احتمال اینکه ولتاژ در بیشتر یا کمتر از یک سطح آستانه مشخص بشود، چقدر است؟
میزان ولتاژ در زمانهای و
به چه طریق با هم ارتباط خواهند داشت؟ به عبارت دیگر، همبستگی به چه شکل خواهد بود؟
خلاصه معیارهای آماری توصیف کننده
معیارهای آماری مختلفی برای جمعآوری، بازبینی، تحلیل و استخراج نتایج مطلوب از سیگنالهای تصادفی در دسترس است. برخی از این معیارهای آماری به طور خلاصه در ادامه آمده است.
معیارهای کمّی مربوط به شکل سیگنال
در بسیاری از تحلیلهای آماری، کار اصلی، به نوعی بدست آوردن یک ایده کلی درباره شکل توزیع سیگنال است که از طریق گشتاورها (moments) انجام میشود.
معیار تمایل به مرکز – میانگین – گشتاور اول
معیارهای تمایل به مرکز تلاش میکنند تا موقعیت مرکزی نمونههای توزیع را که سیگنال تصادفی را بوجود میآورند، تشخیص دهند. میانگین، مد (mode) و میانه (median) معیارهای تمایل به مرکز مختلف هستند. در پردازش سیگنال، بیش از همه به محاسبه میانگین علاقمند هستیم که مقدار متوسط نمونههای داده شده سیگنال است. با داشتن یک متغیر تصادفی با تابع توزیع احتمال
مقدار متوسط به شکل زیر محاسبه میشود:
معیار پراکندگی – واریانس – گشتاور دوم
معیار پراکندگی، نحوه پراکنده شدن مقادیر نمونههای سیگنال را حول یک مکان مرکزی توصیف میکند. واریانس و انحراف معیار (standard deviation) دو مورد از معیارهای پراکندگی هستند. اگر مقادیر به طور وسیع پراکنده باشند، مکان مرکزی، با قدرت کمتری توان نمایش مقادیر را به صورت جامع خواهد داشت. اگر مقادیر به طور فشرده پراکنده باشند، مکان مرکزی بیشتر قابل اعتماد است.
برای متغیر تصادفی گسسته با تابع توزیع احتمال
، مقدار واریانس (
) توسط گشتاور مرکزی دوم محاسبه میشود. عبارت گشتاور مرکزی حاکی از آن است که این مقدار نسبت به میانگین اندازهگیری و محاسبه میشود. برای یک سیگنال الکتریکی، گشتاور دوم متناسب با توان متوسط است:
ریشه مجذور واریانس نیز انحراف معیار است:
شکل 2 نحوه استفاده از هیستوگرام برای بدست آوردن یک درک تصویری از شکل توزیع نمونههای دو سیگنال تصادفی متفاوت را نشان میدهد. اگرچه سیگنالها در حوزه زمان به طور طبیعی مشابه یکدیگر به نظر میرسند، هیستوگرام آنها تصاویر متفاوتی را آشکار میکند. مکان مرکزی (میانگین) سیگنال اول حول مقدار صفر است (جابهجایی جریان ثابت – DC – در نمایش حوزه زمان نداریم) و برای سیگنال دوم مقدار میانگین 0.75 است. توان متوسط سیگنال اول در مقایسه با توان متوسط سیگنال دوم به طور وسیع تغییر میکند (هیستوگرام به طور وسیع پراکنده شده است).
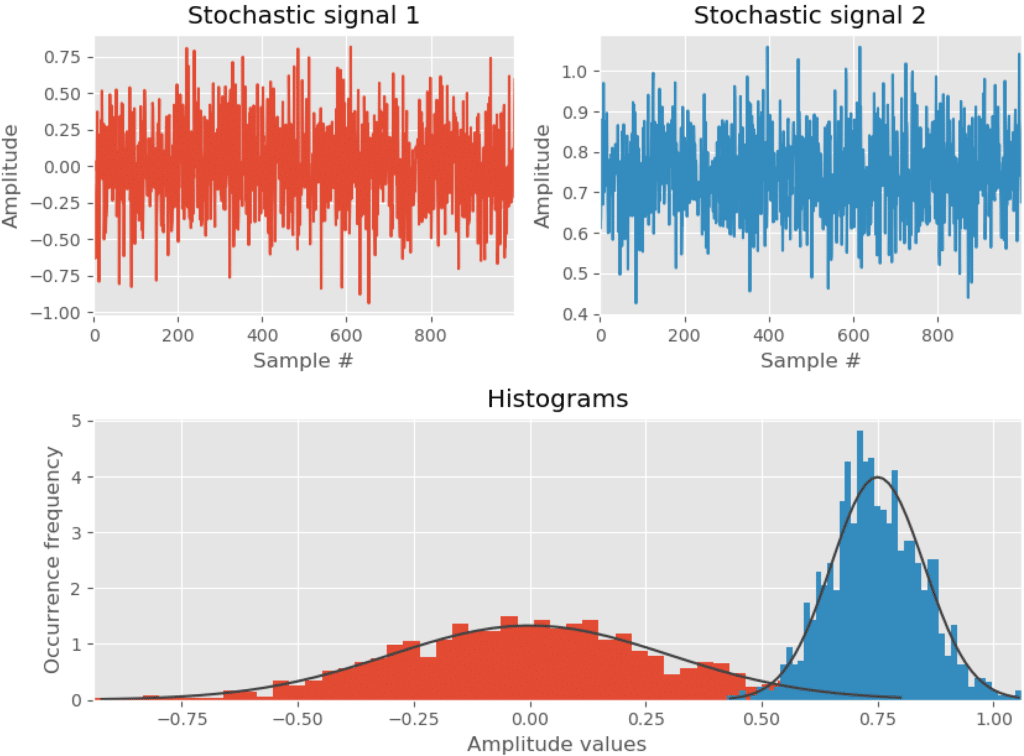
شکل 2- هیستوگرام یک روش بصری است که ایده کلی درباره شکل یک توزیع احتمال را ارائه میکند
گشتاورهای مرتبه بالاتر – چولگی و کشیدگی
توصیف بیشتر شکل توزیع شامل گشتاورهای مرتبه بالاتر میشود: چولگی و کشیدگی. این دو مقدار، ناهنجاریها و نمونههای پرت و دورافتاده در بسیاری از کاربردهای پردازش سیگنال را تشخیص میدهند.
چولگی معیاری برای شناسایی حضور عدم تقارن در شکل توزیع است. در واقع، چولگی اندازه نسبی بخشهای انتهایی توزیع را اندازهگیری میکند. حضور عدم تقارن در توزیع به شکل مقدار غیر صفر برای گشتاور مرکزی مرتبه سوم استاندارد خود را نشان میدهد. عبارت استاندارد معرف نرمالیزه کردن گشتاور مرکزی مرتبه سوم با مقدار است.
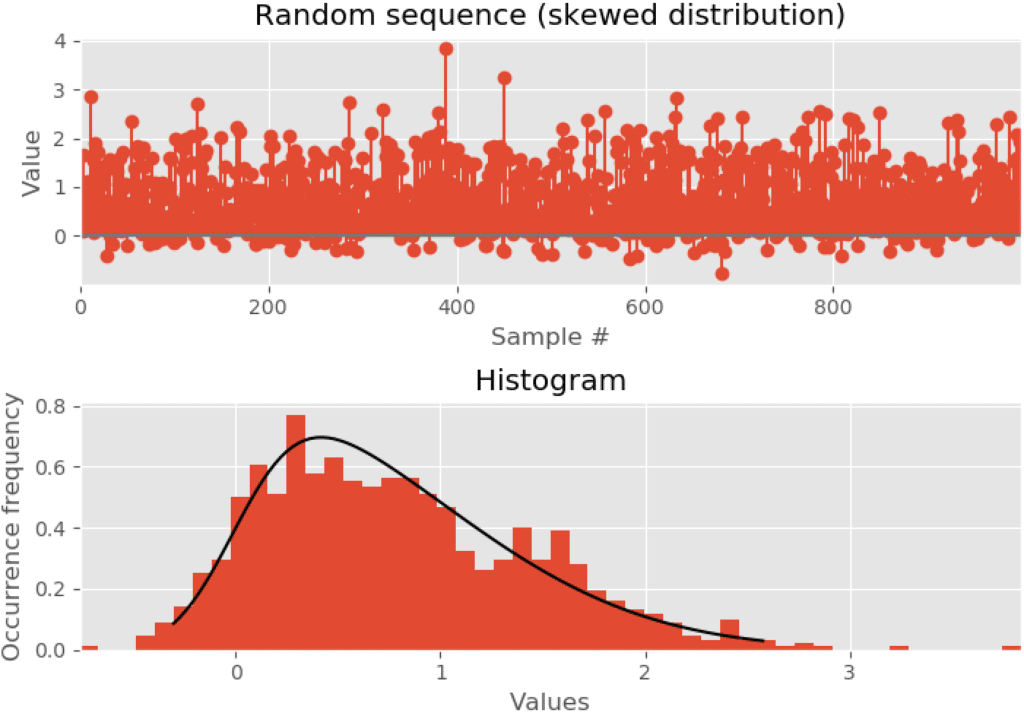
شکل 3- یک دنباله تصادفی با چولگی مثبت (عدم تقارن در شکل) در توزیع
کشیدگی، مقدار احتمال در دو بخش انتهایی توزیع را نسبت به توزیع نرمال با واریانس یکسان، اندازهگیری میکند. کشیدگی برای توزیع نرمال مقدار 3 دارد (منحنی به شکل زنگ کامل). اگر مقدار کشیدگی توزیع بیشتر از 3 شود، نشان دهنده آن است که بخشهای انتهایی نسبت به توزیع نرمال سنگینتر هستند. مقدار کمتر از 3 برای کشیدگی نیز نشان دهنده بخشهای انتهایی سبکتر نسبت به توزیع نرمال است. ضرورتا، کشیدگی معیاری از نقاط پرت است. کشیدگی به صورت گشتاور مرکزی مرتبه چهارم استاندارد محاسبه میشود.
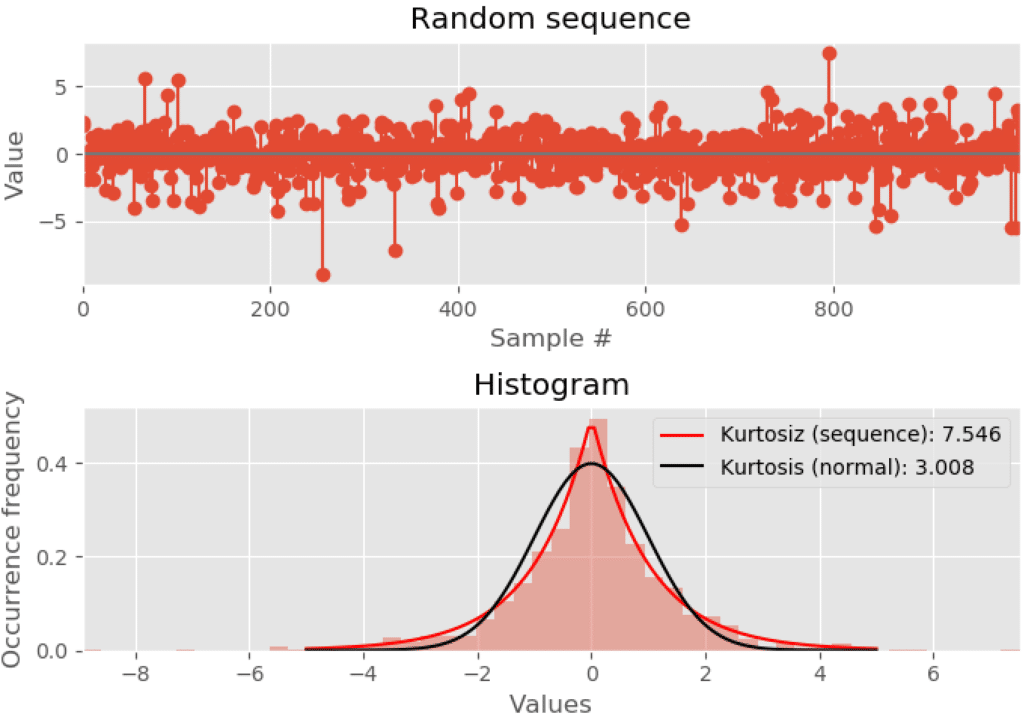
شکل 4- هیستوگرام نشان دهنده کشیدگی یک دنباله تصادفی در مقایسه با کشیدگی یک توزیع نرمال
معیارهای رابطهای
آمارههایی همچون معیارهای تمایل مرکزی، پراکندگی و گشتاورهای مرتبه بالا، که درباره یک توزیع اطلاعاتی را میدهند، تحت عنوان آمارههای تکمتغیره شناخته میشوند. اگر علاقمند به درک رابطه بین دو یا چند متغیر باشیم، باید حداقل به قلمرو آمارههای دومتغیره وارد شویم.
معیارهای رابطهای اندازه رابطه بین دو متغیر را به طور خلاصه بیان میکنند. اغلب معیارهای رابطهای به محدوده مقادیر سیگنال تغییر مقیاس داده میشوند. برای مثال، یک معیار رابطهای میتواند بین 0 تا 1 باشد که مقدار 0 حاکی از عدم ارتباط و مقدار 1 نشان دهنده ارتباط کامل بین دو متغیر تحت مطالعه است. در یک مورد دیگر ممکن است معیار رابطهای در محدوده 1- تا 1+ باشد؛ که میتواند برای تعیین اینکه آیا دو متغیر رابطه مثبت یا منفی با یکدیگر دارند، به ما کمک کند.
نمودار پراکندگی
نمودار پراکندگی راه بسیار خوبی برای ارزیابی بصری از ماهیت رابطه بین دو متغیر است. شکل زیر حاوی نمودارهای پراکندگی بین سیگنالهای تصادفی مختلف است که میزان رابطه بین سیگنالها را نشان میدهد.
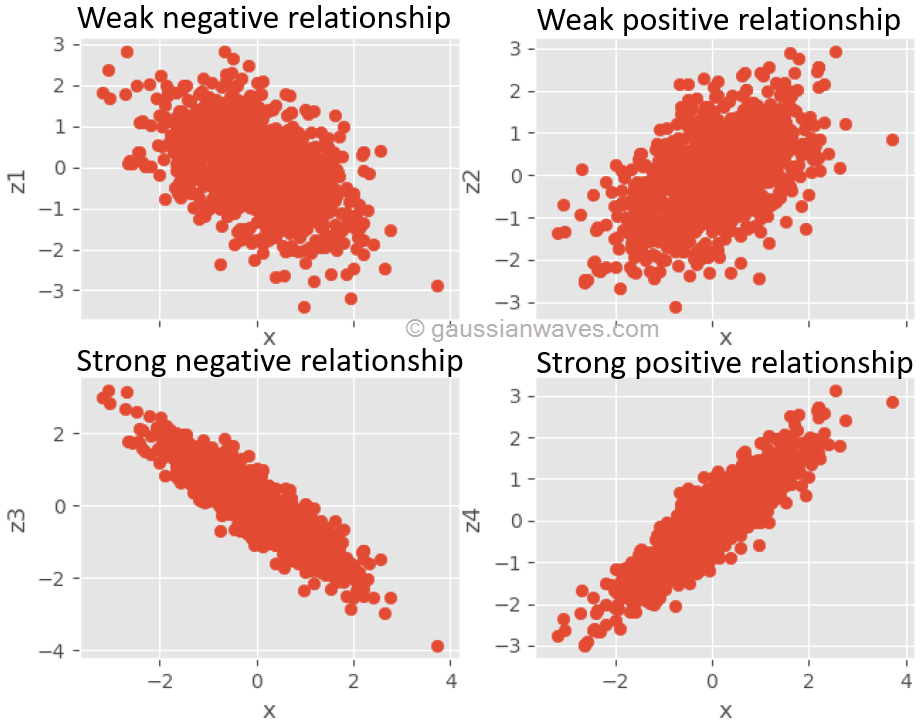
شکل 5- نمودار پراکندگی سیگنالهای تصادفی که نشان دهنده میزان رابطه بین سیگنالهای مختلف است.
همبستگی
توابع همبستگی معمولا در پردازش سیگنال به منظور اندازهگیری تشابه دو سیگنال استفاده میشوند. آنها به طور خاص در تشخیص سیگنال (signal detection) و شناسایی الگو (pattern recognition) مورد استفاده قرار میگیرند.
همبستگی متقابل
همبستگی متقابل معمولا برای اندازهگیری تشابه دو سیگنال مختلف استفاده میشود. در پردازش سیگنال، همبستگی متقابل، تشابه بین دو شکل موج را به صورت تابعی از تاخیرهای زمانی اعمال شده به یکی از آنها اندازهگیری میکند.
برای شکل موجهای زمان-گسسته و
، همبستگی متقابل به شکل زیر تعریف میشود:
که در آن * عمل مزدوج مختلط را نشان میدهد و تاخیرهای زمانی اعمال شده به یکی از شکل موجها است. به عبارت دیگر، همبستگی متقابل به صورت ضرب نقطهای یک دنباله در نسخه شیفت زمانی داده شده دنباله دیگر قابل محاسبه است.
خود همبستگی
خود همبستگی همان همبستگی متقابل یک شکل موج یا دنباله با خودش است. برای شکل موج زمان-گسسته خودهمبستگی به صورت زیر تعریف میشود:
که در آن * عمل مزدوج مختلط است و تاخیرهای زمانی گسستهای است که به نسخه کپی همان شکل موج اعمال شده است.
خواص همبستگی برای تشخیص/تمایز یک دنباله بیت آشنا از یک مجموعه از دنبالههای آشنای محتمل دیگر مناسب و مفید است. برای مثال، در فناوری موقعیتیاب جهانی (GPS) به هر ماهواره یک دنباله کد طلایی 10بیتی اختصاص داده میشود ( ترکیب ممکن). همبستگی متقابل بین کدهای مختلف خیلی کم است زیرا کدهای طلایی نسبت به هم متعامد هستند. هر چند که، خود همبستگی یک کد طلایی در تاخیر صفر حداکثر خواهد بود. ماهوارهها بوسیله این خواص همبستگی کدهای طلایی تشخیص داده میشوند.
نمودارهایی که در ادامه آمده است کاربرد خود همبستگی را برای تحلیل صوت نشان میدهد. خود همبستگی یک سیگنال صوتی در تاخیر صفر (زمانیکه شیفت زمانی در محاسبه همبستگی وجود ندارد) همانطور که در شکل 6 نشان داده شده است، حداکثر است. شکل 7 شامل همان فایل صوتی است که این بار به طور ساختگی مورد پردازش قرار گرفته است تا خواص انعکاسی پیدا کند. با نگاه به نمودار سری زمانی شکل 7، ما نمیتوانیم چیزی استنباط کنیم. در حالیکه، نمودار خود همبستگی خواص انعکاسی نهفته در صوت را آشکار میکند.
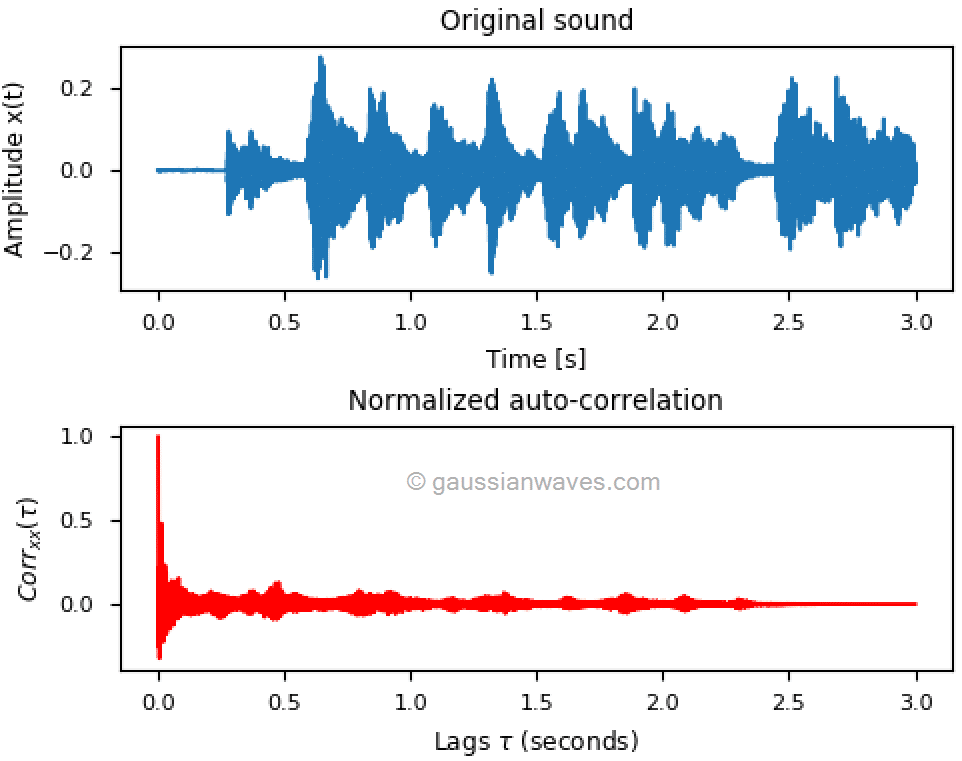
شکل 6- خود همبستگی نرمالیزه شده سیگنال صدای اصلی
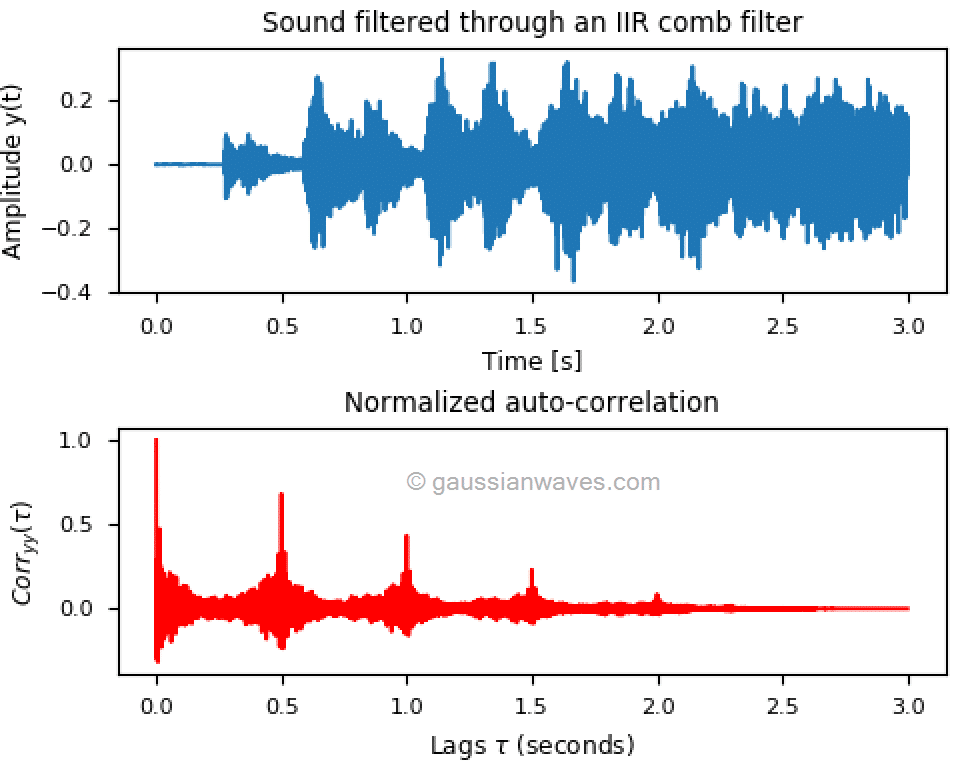
شکل 7- خود همبستگی نرمالیزه شده سیگنال صدای شبیهسازی شده با خواص انعکاسی (پردازش شده به صورت ساختگی با فیلتر شانه IIR)
منبع: www.gaussianwaves.com

دیدگاه ها (2)
سلام خداقوت
ضمن سپاس و قدرانی،توضیحات بسیار ساده و روان و قابل لمسی در مورد موضوع فرآیندهای تصادفی و استفاده از تحلیل آماری در این باره بود.
ممنونم
از توجه شما سپاسگزارم