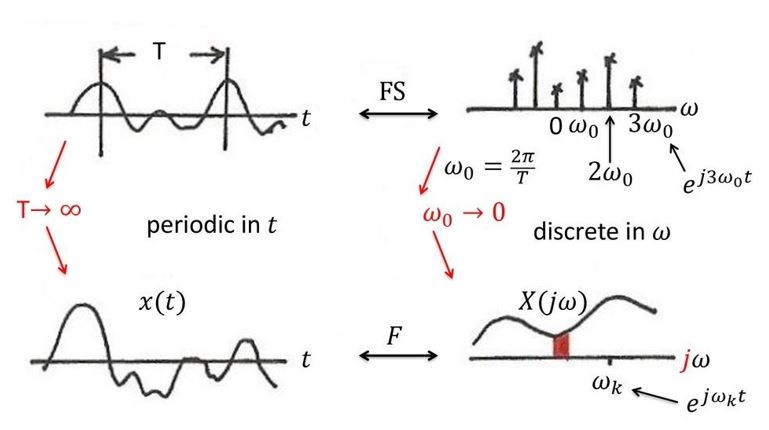
تبدیل فوریه برای زمان-فرکانس به شکل پیوسته-گسسته

تبدیل فوریه برای سیگنالهای زیر قابل تعریف است:

پیوسته یا گسسته در زمان
محدود یا نامحدود در طول زمان

نتایج تبدیل چنین سیگنالهایی 4 حالت است. همانطور که ممکن است انتظار داشته باشید، حوزه فرکانس نیز چنین حالتهایی را دارد:

پیوسته یا گسسته در فرکانس
محدود یا نامحدود در طول فرکانس

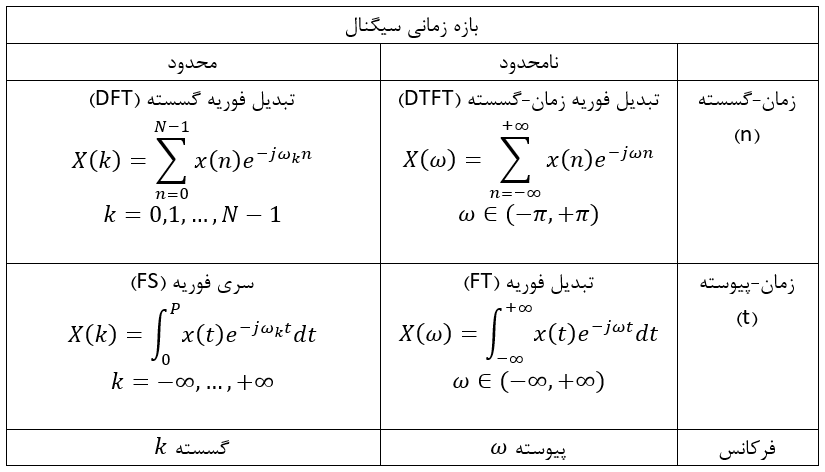
وقتی که سیگنال، زمان-گسسته است، محور فرکانس محدود است و بالعکس، برای سیگنال پیوسته در حوزه زمان، محور فرکانس نامحدود است. جدول زیر این 4 حالت تبدیل فوریه را به طور خلاصه نشان میدهد:

جدول 2-1

در تمام 4 حالت، تبدیل فوریه به شکل یک ضرب داخلی بین سیگنال $x$ با سینوسی مختلط در فرکانس زاویه‌ای $\omega$ قابل تفسیر است:

$X(\omega)=\left \langle x,s_\omega \right \rangle$

که $s_\omega$ به طور مناسب انتخاب و تطبیق داده شده است:

$\\ s_\omega(t) = e^{j\omega t} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (Fourier\ Transform) \\ \\ s_{\omega _k} = e^{j\omega_k t_n} = e^{j2\pi nk/N} \ (DFT) \\ \\ s_\omega(t_n) = e^{j\omega t_n} = e^{j\omega n} \ \ \ (DTFT)$

یک نکته مهم در کاربرد عملی این است که مثلا در مدلسازی طیفی سیگنالهای صوتی، معمولا با سیگنالهای با طول زمانی بسیار زیاد (تقریبا نامحدود) سروکار داریم. تحلیل فوریه یک سیگنال زمان-گسسته نامحدود با استفاده از تبدیل فوریه زمان-گسسته (DTFT) انجام میشود. در ادامه، DTFT تعریف میشود و برخی تئوریهای مرتبط با آن مطرح شده و اثبات میشوند. به علاوه، برای تکمیل بحث، تبدیل فوریه پیوسته (FT) نیز تعریف شده و برخی تئوریهای مرتبط با آن مطرح شده و ثابت میشوند.

تبدیل فوریه زمان-گسسته (DTFT)

تبدیل فوریه DTFT به شکل تبدیل فوریه گسسته (DFT) در حالت حدی که طول N در آن به سمت بینهایت رفته است قابل تصور است:

$X(\omega)\equiv \sum_{n=-\infty}^\infty x(n)e^{-j\omega n}$

که $\omega \in [-\pi,+\pi)$ نشان میدهد که متغیر فرکانس زاویه‌ای پیوسته است و $x(n)$ اندازه دامنه سیگنال برای نمونه شماره $n$ ام است.

معکوس DTFT عبارت است از:

$x(n)=\frac{1}{2\pi}\int_{-\pi}^\pi X(\omega) e^{j\omega n}d\omega$

به جای کار بر روی سیگنال نمونه‌برداری شده با طول $N$ (مشابه DFT)، تبدیل DTFT بر روی سیگنالهای نمونه‌برداری شده $x(n)$ که برای تمام ارقام صحیح تعریف شده است، کار میکند.

برخلاف DFT، فرکانسهای DTFT یک محدوده پیوسته ایجاد میکنند. به عبارت دیگر، DTFT یک تابع پیوسته از فرکانس $\omega \in [-\pi,+\pi)$ است در حالیکه DFT یک تابع گسسته از فرکانس گسسته $k\in [0,N-1] \ , \omega_k$ است. فرکانسهای DFT شامل $k=0,1,2,...,N-1 \ ,\omega_k=2\pi k/N$ است که توسط زوایای $N$ نقطه متقارن روی دایره مختلط واحد در صفحه اعداد مختلط توزیع شده‌اند، تعریف میشوند. بنابراین، با میل کردن $N$ به سمت بینهایت، محور فرکانسی پیوسته به دایره مختلط واحد ختم میشود. این محور همچنان در طول محدود است زیرا حالت نمونه‌برداری شده در حوزه زمان سر جای خود باقی است.

تبدیل فوریه (FT) و معکوس آن

تبدیل فوریه یک سیگنال زمان-پیوسته $x(t) \in \mathbb{C}$ که $t \in (-\infty, \infty)$ به شکل زیر تعریف میشود:

$X(\omega)\equiv \int_{-\infty}^\infty x(t)e^{-j\omega t}dt$

و معکوس آن به شکل

$x(t)=\frac{1}{2\pi}\int_{-\infty}^\infty X(\omega)e^{j\omega t}dt$

بنابراین تبدیل فوریه برای سیگنال زمان-پیوسته به صورت فرکانس-پیوسته تعریف میشود که هر دو محور نیز نامحدود هستند. در نتیجه، سوالات ریاضی همچون وجود تبدیل و معکوس‌پذیری در این حالت بسیار دشوارتر هستند. در حقیقت، چنین سوالهایی دهه‌ها باعث بروز سردرگمی در تاریخ تحلیل هارمونیکی سیگنالها شده است.

وجود تبدیل فوریه

شرایط برای وجود تبدیل فوریه به طور کلی پیچیده است اما کافی است که سیگنال $x(t)$ به طور مطلق انتگرالپذیر باشد:

$\left \| x \right \|_1 \equiv \int_{-\infty}^\infty \left | x(t) \right |dt< \infty$

این نیاز به شکل $x \in L1$ قابل بیان است که بدین معنی است که $x$ متعلق به مجموعه تمام سیگنالهایی است که اندازه $L1$ محدود دارند ( $\left \| x \right \|_1 <\infty$ ). به طور مشابه کافی است که سیگنال $x(t)$ به صورت مجذور نیز انتگرالپذیر باشد:

$\left \| x \right \|_2^2 \equiv \int_{-\infty}^\infty \left | x(t) \right | ^2dt< \infty$

یا $x \in L2$ . به طور کلی‌تر، کافی است نشان دهیم که $1\leq p\leq 2, \ x \in Lp$ .

البته سوال در مورد وجود تبدیل فوریه برای سیگنالهای دنیای واقعی در عمل هرگز مطرح نخواهد شد. هر چند که، سیگنالهای ایده‌آل همچون سینوسی‌ها که در زمان تا بینهایت ادامه دارند، دچار مسائل و مشکلات مربوط به نرمال‌سازی میشوند. در تحلیل مهندسی کاربردی، این مشکلات با استفاده از توابع عام دیراک همچون تابع ضربه (که با آن تابع دلتا نیز میگوییم) حل میشوند.

تئوریهای فوریه برای تبدیل DTFT

این بخش برخی تئوریهای فوریه برای تبدیل فوریه DTFT را به صورت منتخب و گزیده ارائه و اثبات میکند. همانطور که قبلا نیز اشاره شد، تبدیل فوریه زمان-گسسته به شکل زیر تعریف میشود:

$X(\omega)\equiv \sum_{n=-\infty}^{\infty}x(n)e^{-j\omega n}$

در اینجا $X$ طیف سیگنال $x$ است.

خطی بودن DTFT

$\alpha x_1 + \beta x_2 \leftrightarrow \alpha X_1+\beta X_2$

یا

$DTFT(\alpha x_1 + \beta x_2)= \alpha.DTFT(x_1)+\beta .DTFT(x_2)$

که $b,a$ هر عدد اسکالری میتواند باشد (حقیقی یا مختلط)، $x_1$ و $x_2$ نیز دو سیگنال زمان-گسسته دلخواه (توابع با مقدار حقیقی یا مختلط از اعداد صحیح) هستند و $X_2,\ X_1$ طیف فرکانس-پیوسته متناظر آنها هستند که روی دایره واحد در صفحه اعداد مختلط تعریف شده‌اند.

اثبات: داریم

$\\ DTFT_\omega (\alpha x_1+\beta x_2) \equiv \sum_{n=-\infty}^{\infty} [\alpha x_1(n)+ \beta x_2(n)]e^{-j\omega n} \\ \\ \indent \indent \indent \indent \indent \ \ \ \ = \alpha \sum_{n=-\infty}^{\infty}x_1(n)e^{-j\omega n} + \beta \sum_{n=-\infty}^{\infty}x_2(n)e^{-j\omega n} \\ \\ \indent \indent \indent \indent \indent \ \ \ \ \equiv\alpha X_1(\omega)+\beta X_2(\omega)$

معکوس کردن زمان

برای هر سیگنال مختلط $x(n), n \in (-\infty,+\infty)$ داریم:

$FLIP_n(x)\leftrightarrow FLIP_n(X)$

که در آن: $FLIP_n(x) \equiv x(-n)$

اثبات:

$\\ DTFT_\omega (FLIP(x)) \equiv \sum_{n=-\infty}^{\infty} x(-n) e^{-j\omega n}= \sum_{m=\infty}^{-\infty} x(m) e^{-j(-\omega)m} =X(-\omega) \\ \\ \indent \indent \indent \indent \indent \ \ \ \ \equiv FILP_\omega (X)$

البته $FLIP(x)$ باید شامل مزدوج مختلط نیز باشد. اجازه دهید بنویسیم:

$FLIP_n^{'}(x) \equiv \overline{FLIP_n(x)}=\overline{x(-n)}$

چنین تعریفی را نشان دهد. سپس در این حالت خواهیم داشت:

$FLIP^{'}(x)\leftrightarrow \overline{X}$

اثبات:

$DTFT_\omega(FLIP^{'}(x)) \equiv \sum_{n=-\infty}^{\infty} \overline{x(-n)} e^{-j\omega n} = \sum_{m=\infty}^{-\infty} \overline{x(m)e^{-j\omega m}} \equiv \overline{X(\omega)}$

در حالت خاص برای سیگنالهای حقیقی ( $x(n) \in \mathbb{R}$ ) داریم $FLIP(x)=FLIP^{'}(x)$ ، بنابراین:

$FLIP(x)\leftrightarrow \overline{X}$

به عبارت دیگر، معکوس کردن زمان یک سیگنال حقیقی، طیف آن را مزدوج میکند.

تقارن تبدیل DTFT برای سیگنالهای حقیقی

اغلب (و نه همه) سیگنالهایی که ما در عمل با آنها سروکار داریم، سیگنال حقیقی هستند. در اینجا برخی تقارنهای طیفی مرتبط با سیگنالهای حقیقی را بررسی میکنیم.

DTFT سیگنالهای حقیقی

در بخش قبل نشان دادیم که برای طیف X هر سیگنال حقیقی x رابطه زیر برقرار است:

$FLIP(x)=\overline{X}$

یا:

$x(n) \in \mathbb{R}\leftrightarrow X(-\omega)=\overline{X(\omega)}$

به عبارت دیگر، اگر سیگنال $x(n)$ حقیقی باشد، آنگاه طیف آن تقارن هرمیتی (Hermitian) (تقارن مزدوج) دارد. طیف هرمیتی خصوصیات معادل زیر را دارا است:

بخش حقیقی آن زوج است در حالیکه بخش موهومی فرد است:

$\\ Re \left \{ X(-\omega) \right \} = Re \left \{ X(\omega) \right \} \\ Im \left \{ X(-\omega) \right \} = -Im \left \{ X(\omega) \right \}$

اندازه آن زوج است در حالیکه فاز آن فرد است:

$\\ \left | X(-\omega) \right | = \left | X(\omega) \right | \\ \angle X(-\omega) = -\angle X(\omega)$

دقت کنید که یک تابع زوج، حول محور عمودی متقارن است و یک تابع فرد، حول نقطه مبداء متقارن است.

سیگنالهای زوج (یا فرد) حقیقی

اگر یک سیگنال علاوه بر حقیقی بودن، زوج نیز باشد، آنگاه تبدیل DTFT آن نیز حقیقی و زوج است. این ویژگی از تقارن هرمیتی سیگنالهای حقیقی نتیجه میشود و این حقیقت که تبدیل DTFT هر سیگنال زوج، حقیقی است:

$\\ DTFT_\omega(x) \equiv \sum_{n=-\infty}^{\infty}x(n)e^{-j\omega n} \\ \\ \indent \indent \indent \ =\sum_{n=-\infty}^{\infty}x(n)[cos(\omega n)+j sin(\omega n)] \\ \\ \indent \indent \indent \ = \sum_{n=-\infty}^{\infty}x(n)[cos(\omega n)+j\sum_{n=-\infty}^{\infty}x(n)[sin(\omega n)\\ \\ \indent \indent \indent \ = \sum_{n=-\infty}^{\infty}x(n)[cos(\omega n)\\ \\ \indent \indent \indent \ = real \ and \ even$

این ویژگی برقرار است زیرا تابع کسینوس، زوج است و سینوس فرد، ضرب تابع زوج در زوج، زوج است و ضرب زوج در فرد، فرد و اینکه جمع روی تمام نمونه‌های یک سیگنال فرد، صفر است. یعنی:

$\\ \sum_{n=-\infty}^{\infty} x(n)cos(\omega n) = \sum_{n=-\infty}^{\infty}(even \ in \ n).(doubly \ even) \\ \\ \indent \indent \indent \indent \indent\ = \sum_{n=-\infty}^{\infty}(doubly \ even) = (even \ in \ \omega))$

$\\ \sum_{n=-\infty}^{\infty} x(n)sin(\omega n) = \sum_{n=-\infty}^{\infty}(even \ in \ n).(doubly \ odd) \\ \\ \indent \indent \indent \indent \indent\ = \sum_{n=-\infty}^{\infty}(doubly \ odd) = 0$

اگر x حقیقی و زوج باشد، عبارتهای زیر صحیح است:

$FLIP(x) = x \indent (x(-n)=x(n)) \\ \\ \indent \indent \indent \ \ \overline{x} = x \\ \\ \indent \ FLIP(X) = X \\ \\ \indent \indent \indent \ \ \overline{X} = X \\ \\ \indent \indent \angle X(\omega)= 0 \ or \ \pi$

به طور مشابه، اگر یک سیگنال فرد و حقیقی باشد، آنگاه تبدیل DTFT آن فرد و کاملا موهومی است. این ویژگی نیز از تقارن هرمیتی سیگنالهای حقیقی نتیجه میشود و این نکته که تبدیل DTFT هر سیگنال فرد، موهومی خالص است:

$DTFT_\omega(x) \equiv \sum_{n=-\infty}^{\infty}x(n)e^{-j\omega n} \\ \\ \indent \indent \indent \indent \ =\sum_{n=-\infty}^{\infty}x(n)cos(\omega n)+j \sum_{n=-\infty}^{\infty}x(n) sin(\omega n) \\ \\ \indent \indent \indent \indent \ =j \sum_{n=-\infty}^{\infty}x(n) sin(\omega n) \\ \\ \indent \indent \indent \indent \ = imaginary \ and \ odd$

در اینجا از این حقیقت استفاده شده است که:

$\\ \sum_{n=-\infty}^{\infty} x(n)cos(\omega n) = \sum_{n=-\infty}^{\infty}(odd \ in \ n).(doubly \ even) \\ \\ \indent \indent \indent \indent \indent\ = \sum_{n=-\infty}^{\infty}(odd \ in \ n ,even \ in \ \omega) = 0$

$\\ \sum_{n=-\infty}^{\infty} x(n)sin(\omega n) = \sum_{n=-\infty}^{\infty}(odd \ in \ n).(doubly \ odd) \\ \\ \indent \indent \indent \indent \indent\ = \sum_{n=-\infty}^{\infty}(even \ in \ n ,odd \ in \ \omega) = (odd \ in \ \omega)$

تئوری جابه‌جایی (شیفت) برای DTFT

عملگر جابه‌جایی برای سیگنالهای نمونه‌برداری شده $x(n)$ به صورت زیر تعریف میشود:

$SHIFT_{l,n}(x) \equiv x(n-l)$

که $l$ هر عدد صحیحی میتواند باشد ( $l \in \mathbb{Z}$ ). بنابراین، $SHIFT_l (x)$ یک جابه‌جایی به راست یا تاخیر به اندازه $l$ نمونه است.

تئوری جابه‌جایی میگوید:

$SHIFT_l(x)\leftrightarrow e^{-j(.)l}X$

یا به صورت اپراتوری میتوان نوشت:

$DTFT_\omega[SHIFT_l(x)]= (e^{-j\omega l})X(\omega)$

اثبات:

$DTFT_\omega [SHIFT_l(x)] \equiv \sum_{n=-\infty}^{\infty}x(n-l)e^{-j\omega n} \\ \\ \indent \indent \indent \indent \indent \indent \indent \ = \sum_{m=-\infty}^{\infty}x(m)e^{-j\omega (m+l)} \indent (m \equiv n-l) \\ \\ \indent \indent \indent \indent \indent \indent \indent \ = \sum_{m=-\infty}^{\infty}x(m)e^{-j\omega m} e^{-j\omega l} \\ \\ \indent \indent \indent \indent \indent \indent \indent \ = e^{-j\omega l}\sum_{m=-\infty}^{\infty}x(m)e^{-j\omega m} \\ \\ \indent \indent \indent \indent \indent \indent \indent \ \equiv e^{-j\omega l}X(\omega)$

دقت کنید که $e^{-jwl}$ یک عبارت فاز خطی است زیرا یک تابع خطی از فرکانس با شیف برابر با $-l$ است.

$\angle (e^{-j\omega l}) = -\omega l$

تئوری جابه‌جایی به ما نشان میدهد که ضرب یک طیف فرکانسی $X(\omega)$ با فاز خطی $e^{-jwl}$ متناظر با یک تاخیر در حوزه زمان به اندازه $l$ نمونه است. اگر $l<0$ ، به آن پیشروی زمانی به اندازه $\left | l \right |$ نمونه گفته میشود.

تئوری کانولوشن (convolution) برای DTFT

کانولوشن سیگنالهای زمان-گسسته $x$ و $y$ به شکل زیر تعریف میشود:

$(x*y)(n) \equiv \sum_{m=-\infty}^{\infty}x(m)y(n-m)$

گاهی اوقات این رابطه، کانولوشن غیرحلقوی نیز نامیده میشود تا از کانولوشن حلقوی که برای دنباله‌های با طول $N$ در حوزه تعریف تبدیل فوریه گسسته (DFT) استفاده میشود، متمایز گردد. کانولوشن در حوزه زمان برای تبدیل DFT و سری FS به شکل حلقوی است (برای طول محدود در حوزه زمان) و برای تبدیلهای DTFT و FT غیرحلقوی.

تئوری کانولوشن عبارت است از:

$(x*y)\leftrightarrow X.Y$

به عبارت دیگر، کانولوشن در حوزه زمان متناظر با ضربه نقطه به نقطه در حوزه فرکانس است.

اثبات:

نتیجه فورا از جابه‌جایی مرتبه جمع در فرمول کانولوشن و تبدیل DTFT حاصل میشود:

$\\ DTFT_\omega (x*y) \equiv \sum_{n=-\infty}^{\infty}(x*y)_n \ e^{-j\omega n} \\ \indent \indent \indent \indent \ \equiv \sum_{n=-\infty}^{\infty} \ \sum_{m=-\infty}^{\infty} x(m)y(n-m)e^{-j\omega m} \\ \indent \indent \indent \indent \ \equiv \sum_{m=-\infty}^{\infty} x(m)\sum_{n=-\infty}^{\infty} \underbrace{y(n-m)e^{-j\omega m}} \\ \indent \indent \indent \indent \indent \indent \indent \indent \indent \indent \indent e^{-j\omega m}Y(k) \\ \indent \indent \indent \indent \ = \left ( \sum_{m=-\infty}^{\infty}x(m)e^{-j\omega m} \right ) Y(\omega) \ \ \ (by \ the \ shift \ theorem) \\ \\ \indent \indent \indent \indent \ \equiv X(\omega).Y(\omega)$

تئوری همبستگی متقابل (cross-correlation) برای DFTF

همبستگی متقابل دو سیگنال زمان-گسسته $x$ و $y$ به صورت زیر تعریف میشود:

$(x\star y)_n \equiv \sum_{m}\overline{x(m)} y(m+n)$

تئوری همبستگی برای DTFT عبارت است از:

$x \star y \leftrightarrow \overline{X}.Y$

اثبات:

$\\ (x\star y)_n \equiv \sum_m \overline{x(m)}y(n+m) \\ \indent \indent \ = \sum_m \overline{x(-m)}y(n-m) \indent (m\leftarrow -m) \\ \\ \indent \indent \ =(FLIP(\overline{x})*y)_n \\ \\ \indent \indent \ \leftrightarrow \overline{X}.Y$

که گام آخر از تئوری کانولوشن و تقارن حاصل از تئوری جابه‌جایی، $FLIP(\overline{x})\leftrightarrow \overline{X}$ بدست آمده است.

خودهمبستگی (auto-correlation)

خودهمبستگی یک سیگنال $x$ به سادگی همان همبستگی متقابل سیگنال $x$ با خودش است:

$(x \star x)(n) \equiv \sum_m \overline{x(m)}x(m+n)$

از تئوری همبستگی داریم:

$(x\star x)\leftrightarrow \left | X \right | ^2$

دقت کنید که این تعریف خودهمبستگی برای سیگنالهایی که طول محدود دارند (غیر صفر روی تعداد محدودی از نمونه‌های زمانی هستند) مناسب است. برای سیگنالهای با انرژی نامحدود (ولی توان محدود)، همچون فرآیندهای نویز ایستان، خودهمبستگی نمونه‌ای تعریف میشود که شامل نرمال‌سازی مناسب است.

از تئوری خودهمبستگی میتوان چنین نتیجه گرفت که یک پاسخ ضربه فیلتر دیجیتال $h(n)$ ، مربوط به یک فیلتر تمام‌گذر بدون افت است اگر و تنها اگر $h \star h = \delta \leftrightarrow 1$ . به عبارت دیگر، خودهمبستگی پاسخ ضربه هر فیلتر تمام‌گذر یک ضربه است.

تئوری قدرت برای DTFT

ضرب داخلی دو سیگنال در حوزه زمان به شکل زیر تعریف میشود:

$\left \langle x,y \right \rangle\equiv \sum_{n=-\infty}^{\infty}x_n \overline{y}_n$

ضرب داخلی دو طیف فرکانسی نیز عبارت است از:

$\left \langle X,Y \right \rangle\equiv \frac{1}{2\pi}\int_{-\pi}^{\pi}X(\omega) \overline{Y(\omega)}d\omega$

دقت کنید که ضرب داخلی حوزه فرکانس شامل فاکتور نرمال‌سازی میشود در حالیکه در حوزه زمان چنین نیست.

با استفاده از نماد ضرب داخلی، تئوری قدرت (یا همان تئوری پارسوال – Parseval) برای DTFT میتواند به شکل زیر بیان شود:

$\left \langle x,y \right \rangle\equiv \left \langle X,Y \right \rangle$

به عبارتی، ضرب داخلی دو سیگنال در حوزه زمان، معادل ضرب داخلی طیفهای فرکانسی آنها است (یک عدد اسکالر مختلط در حالت کلی).

زمانیکه ضرب داخلی یک سیگنال با خودش را در نظر میگیریم، ما حالت خاصی تحت عنوان تئوری انرژی (یا تئوری انرژی رایلی – Rayleigh) داریم:

$\left \| x \right \|^2=\left \langle x,x \right \rangle = \left \langle X,X \right \rangle = \left \| X \right \|^2$

که $\left \| . \right \|$ نشان دهنده نرم مرتبه دو یا L2 ناشی از ضرب داخلی است. این مقدار همیشه حقیقی است.

اثبات:

$\\ \left \langle x,y \right \rangle \equiv \sum_{n=-\infty}^{\infty} x(n)\overline{y(n)}=(y\star x)_0 = DTFT_0^{-1}(\overline{Y}.X) \\ \\ \indent \ \ = \frac{1}{2\pi} \int_{-\pi}^{\pi} X(\omega)\overline{Y(\omega)}d\omega \equiv \left \langle X,Y \right \rangle$

عملگر گسترش (stretch) در زمان

ما عملگر گسترش در حوزه زمان را به شکل زیر تعریف میکنیم:

$STRETCH_{L,n}(x) \equiv \left\{\begin{matrix} x(\frac{n}{L}), & n=0\ (MOD \ \ L)\\ \\ 0, & O.W. \end{matrix}\right.$

به عبارت دیگر، یک سیگنال نمونه‌برداری شده را با فاکتور $L$ بوسیله قرار دادن $L-1$ صفر بین هر دو نمونه آن، گسترده میکنیم.

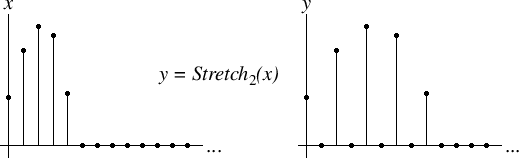
شکل 2-1- نمایش عملگر گسترش

در متون علمی مرتبط با بانک فیلترها، اصطلاح عملگر گسترش معمولا به جای عملگر افزایش نمونه‌ها (upsampling) استفاده میشود. به عبارتی، گسترش یک سیگنال با فاکتور $K$ ، افزایش نمونه‌های سیگنال با فاکتور $K$ گفته میشود (نمایش گرافیکی آن به شکل $\uparrow K$ است). عبارت “گسترش” در اینجا ترجیح داده شده است زیرا افزایش نمونه‌ها به سادگی با افزایش نرخ نمونه‌برداری اشتباه گرفته میشود که همان نمونه‌برداری مجدد یک سیگنال به نرخ نمونه‌برداری بالاتر است و توسط عملگر گسترش و به دنبال آن یک فیلتر پایین‌گذر ایده‌آل به منظور انتقال صفرهای وارد شده به سیگنال به مقادیر درونیابی شده مناسب، انجام میشود.

دقت کنید که ما میتوانیم عملگر گسترش را عملگر مقیاس‌دهی نیز بنامیم که در این صورت این مفهوم در حوزه زمان-گسسته با معادل آن در حوزه زمان-پیوسته متحد میشود.

عملگر تکرار (مقیاس دهنده)

ما عملگر تکرار در حوزه فرکانس را به صورت یک تغییر مقیاس محور فرکانس با فاکتور صحیح $L>0$ نشان میدهیم:

$REPEAT_{L,\nu}(X)\equiv X(L\omega), \indent \omega \in \left [ -\frac{\pi}{L}, \frac{\pi}{L}\right )$

که $\nu =L\omega \in [-\pi,\pi)$ متغیر فرکانس زاویه‌ای را بعد از اعمال عملگر تکرار نشان میدهد. عملگر تکرار، تمام دایره واحد (از $-\pi$ تا $\pi$ ) را به بخشی از خودش $[-\pi/L,\pi/L)]$ نگاشت میدهد که به مرکز $\omega =0$ است و $L$ مرتبه تکرار شده است. این موضوع در شکل 2.2 برای $L=3$ نشان داده شده است.

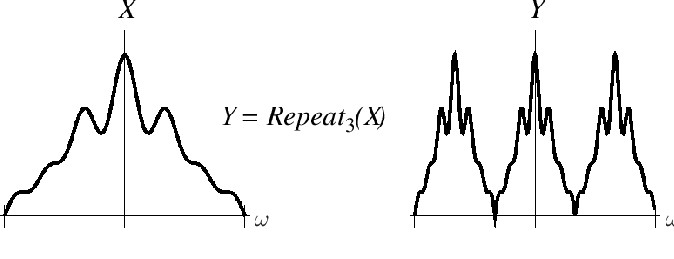
شکل 2-2- نمایش عملگر تکرار

از آنجا که محور فرکانس پیوسته است و برای DTFT دوره تناوب $2\pi$ دارد، عملگر تکرار دقیقا معادل یک عملگر تغییر مقیاس برای حالت تبدیل فوریه عادی است. این عملگر را ما به جای مقیاس، همان تکرار میگوییم زیرا ما در حال محدود کردن فاکتور مقیاس به اعداد مثبت هستیم، و همچنین نام تکرار، آنچه که در مورد یک طیف متناوب رخ میدهد را بهتر نشان میدهد که همان تغییر مقیاس در حوزه فرکانس به طور فشرده روی دایره واحد با یک فاکتور صحیح است.

تئوری گسترش/تکرار (تغییر مقیاس)

با استفاده از تعاریف قبلی، حال میتوانیم به طور مختصر تئوری گسترش را بیان کنیم:

$STRETCH_L(x)\leftrightarrow REPEAT_L(X)$

اثبات:

$\\ DTFT_\omega[STRETCH_L(x)] \equiv \sum_{n=-\infty}^{\infty}STRETCH_{L,n}(x)e^{-j\omega n}) \\ \\ \indent \indent \indent \indent \indent \indent \indent \ \ = \sum_{m=-\infty}^{\infty}x(m)e^{-j\omega mL}) \indent (m\equiv n/L) \\ \\ \indent \indent \indent \indent \indent \indent \indent \ \ \equiv X(\omega L)$

همانطور که $\omega$ ، بازه $[-\pi,\pi)$ را طی میکند، $X(\omega L)$ دایره واحد را $L$ مرتبه طی میکند، بنابراین عملگر تکرار را روی دایره واحد پیاده‌سازی میکند. دقت کنید که زمانیکه $\omega =0$ ، داریم: $\omega L=0$ ، بنابراین مقدار DC یا همان ثابت، همواره به مقدار DC نگاشت داده میشود. در مقدار نصف نرخ نمونه‌برداری، $\omega =\pm \pi$ است، از طرفی، بعد از نگاشت، ممکن است داشته باشیم: $Y(\pi)=X(-\pi)$ (برای $L$ فرد)، یا $X(0)$ (برای $L$ زوج)، که $Y(\omega)\equiv X(\omega L)$ .

تئوری گسترش نحوه تبدیل یا تغییر نرخ نمونه‌برداری ایده‌آل را برای نسبتهای صحیح افزایش سرعت نمونه‌برداری مشخص میکند: ابتدا سیگنال با فاکتور $L$ گسترده میشود (با افزودن $L-1$ صفر بین هر دو نمونه مجاور هم)، سپس فیلتر پایین‌گذر ایده‌آل با فرکانس قطع $\pi/L$ به آن اعمال میشود. چنین سیستمی (اگر قابل پیاده‌سازی باشد)، درونیابی باند محدود (bandlimited interpolation) سیگنال اصلی با فاکتور $L$ را پیاده‌سازی میکند.

تئوری گسترش مشابه تئوری تغییر مقیاس برای تبدیل فوریه پیوسته است که در بخشهای بعدی معرفی میشود.

منبع: www.dsprelated.com

تبدیل فوریه برای زمان-فرکانس به شکل پیوسته-گسسته

دیدگاه ها (0)

لغو پاسخ