نکاتی درباره نمونه‌برداری سیگنال

نکاتی درباره نمونه‌برداری سیگنال

چندی پیش با مساله جالبی مواجه شدم. در توصیف فرآیند نمونه‌برداری، نمایش نمونه‌برداری با تابع ضربه مطابق شکل زیر تقریبا در هر کتاب درسی پردازش سیگنال دیجیتال یا مخابرات دیده میشود. حال سوالی که مطرح میشود، این است: چگونه ممکن است پس از نمونه‌برداری، محور فرکانس با ضریب $\frac{1}{T_s}$ که مقداری بسیار بزرگ است، مقیاس‌بندی شود؟ برای یک مبدل آنالوگ به دیجیتال (ADC) که به طور مثال با سرعت 10 مگاهرتز کار میکند، اندازه دامنه طیف فرکانسی و تکرارهای آن در حدود 10 به توان 7 میشود! به نظرم آمد که باید چیزی در جایی غلط باشد.

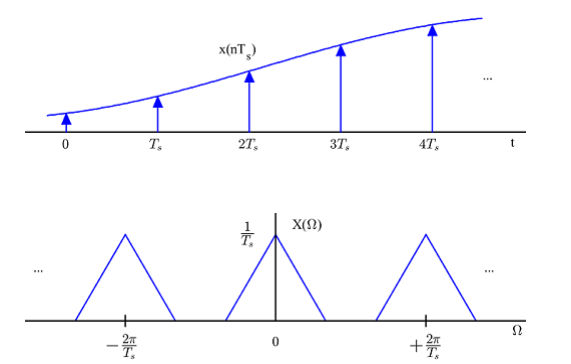
شکل 1- نمونه‌برداری در حوزه زمان، طیف فرکانسی را در حوزه فرکانس تکرار میکند که هر کدام با مقدار $\frac{1}{T_s}$ تغییر مقیاس داده شده است.

سوال خود را از چند متخصص DSP پرسیدم. آنها جواب را به درستی نمیدانستند. به تدریج خودم شروع به درک علت این موضوع کردم که چرا چنین چیزی باید درست باشد. پاسخ بسیار صریح و واضح است که در نگاه اول آن را متوجه نشدم. در ادامه مسیری را که منجر به درک این رخداد شد، ارائه کرده‌ام.

یک ضربه واحد

اولین نکته جالب این بود که هر جا توابع ضربه حضور دارند، هر آنچه که از آن به بعد ظاهر میشود کمی مرموز خواهد بود. یک تابع ضربه پیوسته به شکل زیر تعریف میشود.

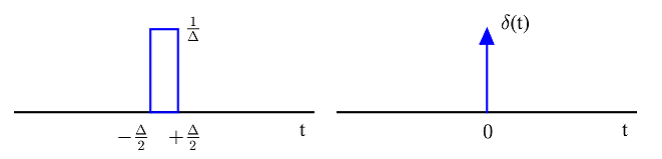
مساحت زیر مستطیل: $\int_{-\infty }^{+\infty }\delta (t)=1$ یا $\Delta \frac{1}{\Delta}=1$

شکل 2- تعریف تابع ضربه واحد

واضح است که فاکتور تغییر مقیاس نمونه‌برداری، مستقل از نحوه تعریف تابع ضربه و ارتفاع نامحدود آن است. در مرحله بعد، نگاهی به دنباله ضربه‌های با دامنه واحد می‌اندازیم: قطار ضربه.

قطار ضربه

یک قطار ضربه، دنباله‌ای از ضربه‌ها با دوره تناوب $T_s$ است که به شکل زیر تعریف میشود:

$p(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT_s)$

روش استاندارد برای بدست آوردن تبدیل فوریه از طریق نمایش سیگنال متناوب بالا به صورت سری فوریه و سپس یافتن ضرایب سری فوریه است. در ابتدا، لازم به ذکر است که سیگنال $x(t)$ با تناوب $T_s$ به شکل زیر بیان میشود:

$x(t)=\sum_{k=-\infty}^{+\infty}x_k e^{jk\Omega _st}$

که در آن $\Omega _s=\frac{2\pi }{T_s}$ به عنوان هارمونیک اصلی در دنباله فرکانسی $k\Omega _s$ که $k$ در محدوده $-\infty$ تا $+\infty$ تغییر میکند، است. در اینجا، $x_k$ ها ضرایب سری فوریه هستند که از فرمول زیر حاصل میشوند:

$x_k=\frac{1}{T_s}\int_{-\frac{T_s}{2}}^{\frac{T_s}{2}}x(t)e^{-jk\Omega _st}dt$

زمانیکه $p(t)$ یک قطار ضربه است، بازه زمانی یک تناوب بین $-\frac{T_s}{2}$ و $+\frac{T_s}{2}$ فقط شامل یک ضربه $\delta (t)$ است. بنابراین، $p_k$ به شکل زیر محاسبه میشود:

$p_k=\int_{-\frac{T_s}{2}}^{+\frac{T_s}{2}}\delta(t)e^{-jk\Omega_st}dt=\frac{1}{T_s}e^{-jk\Omega_s0}=\frac{1}{T_s}$

با لحاظ کردن فرمول بالا در تعریف گفته شده و با توجه به اینکه $F\left \{ e^{jk\Omega_st} \right \}=2\pi\delta(\Omega-k\Omega_s)$ و $\Omega_s=\frac{2\pi}{T_s}$ میتوان نوشت:

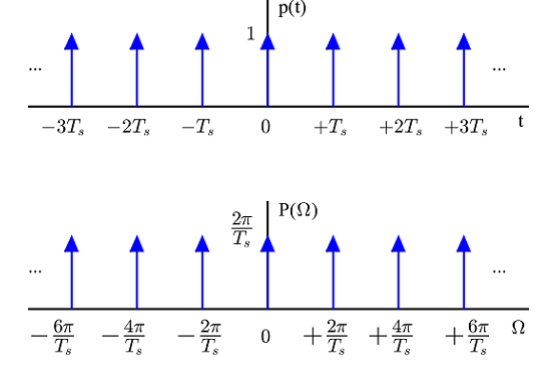
$P(\Omega)=\frac{1}{T_s}\sum_{k=-\infty}^{+\infty}\left \{ e^{jk\Omega_st} \right \}=\frac{2\pi}{T_s}\sum_{k=-\infty}^{+\infty}\delta(\Omega-k\frac{2\pi}{T_s})$

شکل 3- تبدیل فوریه قطار ضربه در حوزه زمان خود قطار ضربه دیگری است در حوزه فرکانس

دنباله‌های بدست آمده در حوزه زمان و فرکانس در شکل بالا نمایش داده شده است که به نوعی یک شکل استاندارد در متون علمی پردازش سیگنال دیجیتال است. هر چند اینکه تبدیل فوریه یک قطار ضربه با وجود ثابت بودن تبدیل فوریه تابع ضربه واحد، خود قطار ضربه دیگری است، موجب تعجب میشود. چه اتفاقی در رابطه با مفهوم داشتن یک طیف وسیع برای سیگنال محدود در حوزه زمان، رخ داد؟ البته با این روش، علت به راحتی روشن نخواهد شد.

بنابراین من به بررسی آن از طریق روش دیگری پرداختم. دقت کنید که در اینجا متغیر $F$ به جای $\Omega$ برای فرکانس استفاده شده است.

$\int_{-\infty}^{+\infty}\sum_{n=-\infty}^{+\infty}\delta(t-nT_s)e^{-j2\pi Ft}dt=\sum_{n=-\infty}^{+\infty}\int_{-\infty}^{+\infty}\delta(t-nT_s)e^{-j2\pi Ft}dt\\=\sum_{n=-\infty}^{+\infty}e^{-j2\pi FnT_s}$

در اینجا، روشهای متعددی برای اثبات رابطه نهایی وجود دارد که بررسی آنها را دشوار میشود. بنابراین فقط از طریق بررسی گرافیکی و اینکه به کجا ختم میشود، پیش میرویم.

ضربه‌ها از کجا می‌آیند

در ابتدا باید گفت که تبدیل فوریه قطار ضربه حوزه زمان میتواند به صورت مجموع سیگنالهای سینوسی مختلط در حوزه فرکانس با فرکانسهای برابر با $nT_s$ یا تناوب برابر با $\frac{1}{nT_s}=\frac{F_s}{n}$ در نظر گرفته شود. همچنین، سیگنال بالا یک سیگنال متناوب با دوره تناوب هارموینک اول برابر با $\frac{1}{T_s}=F_s$ خواهد بود.

$\sum_{n=-\infty}^{+\infty}e^{-j2\pi(F+F_s)nT_s}=\sum_{n=-\infty}^{+\infty}e^{-j2\pi FnT_s} e^{-j2\pi n}=\sum_{n=-\infty}^{+\infty}e^{-j2\pi FnT_s}$

بنابراین، برای نمایش بهتر سیگنال در حوزه فرکانس، خود را به بازه $[0,F_s)$ محدود میکنیم. هر آنچه در اینجا اتفاق می‌افتد در جاهای دیگر نیز تکرار خواهد شد. شکل 4، سه سیگنال سینوسی مختلط حوزه فرکانس $e^{-j2\pi FnT_s}$ برای $n=1,2,3$ با فرکانسهای $T_s,2T_s,3T_s$ را به ترتیب نمایش میدهد. دقت کنید که چگونه در یک تناوب $F_s$ ، سیگنال اول یک سیکل را کامل میکند در حالیکه دو سیگنال دیگر به ترتیب 2 و 3 سیکل را کامل میکنند. در اینجا، عمدا از رسم شکل برای $n=0$ اجتناب کرده‌ایم زیرا یک خط مستقیم در راستای محور I خواهد بود.

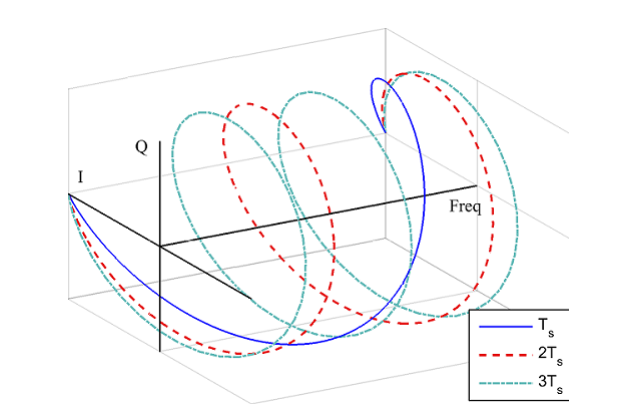
شکل 4- سه سیگنال سینوسی مختلط در حوزه فرکانس $e^{-j2\pi FnT_s}$ برای $n=1,2,3$ با فرکانسهای $T_s,2T_s,3T_s$ در بازه $[0,F_s)$

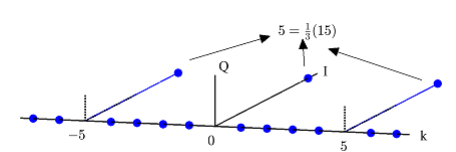
در نمای نزدیکتر، تجزیه سیگنال به بخشهای I و Q را ملاحظه کنید. به وضوح، محور I شامل $cos(2\pi FnT_s)$ و محور Q شامل $-sin(2\pi FnT_s)$ برای $n=1,2,3$ است که در شکل 5 نشان داده شده است.

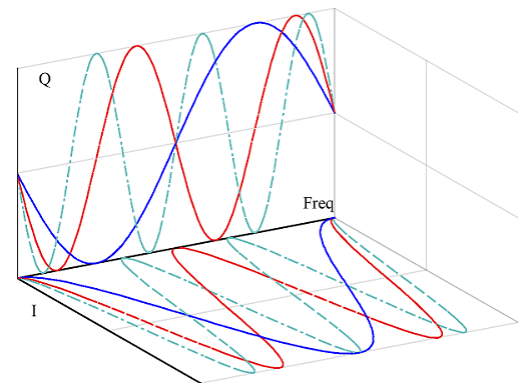
شکل 5- تجزیه سیگنالهای شکل 4 به بخشهای I و Q. محور I شامل $cos(2\pi FnT_s)$ و محور Q شامل $-sin(2\pi FnT_s)$ است برای $n=1,2,3$ در محدوده $[0,F_s)$

با فرض دانستن مفاهیم پایه، حال محدوده $[0,F_s)$ را به $N$ بخش با پهنای $\nu$ تقسیم میکنیم:

$\nu = \frac{F_s}{N}$

میتوان نوشت که برای عدد صحیح $k$

$F\approx k\nu =k\frac{F_s}{N}, fT_s=\frac{k}{N}$

نتیجه جمع سیگنالهای سینوسی نشان داده شده در شکل 5 برای عدد بزرگ $N$ در شکل 6 آمده است.

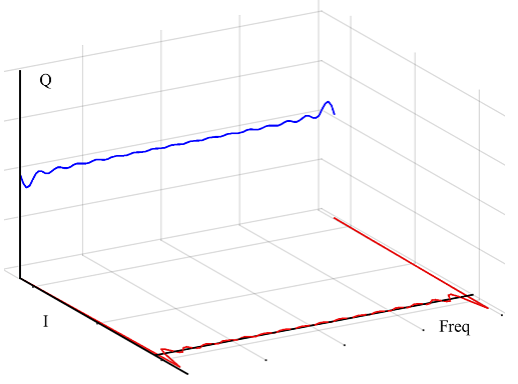
شکل 6- جمع بخشهای I و Q از شکل 5 برای مقدار $N$ بزرگ در بازه $[0,F_s)$ . بخش Q به صفر همگرا میشود در حالیکه بخش I به یک ضربه نزدیک میشود که نیمی از آن در مقدار صفر و نیم دیگر در $F_s$ قابل مشاهده است.

مستطیل ضربه در $k=0$ ارتفاع $N$ دارد زیرا جمع $N$ مقدار 1 برای $n$ های مختلف است. بنابراین میتوان نتیجه گرفت که:

بازوی I – عبارت سیگما $\sum_{n=-\infty}^{+\infty}cos(2\pi nk/N)$ در $k=0$ و در هر تناوب $[0,F_s)$ به مقدار $N$ میل میکند. وقتی که $\nu \rightarrow 0$ آنگاه $N\rightarrow \infty$ و به شکل یک ضربه درمی‌آید (البته به طور صریح میتوان گفت که این حد به صورت یک تابع وجود ندارد و در واقع به شکل یک توزیع است).
از طرف دیگر، بازوی Q – عبارت سیگما $\sum_{n=-\infty}^{+\infty}-sin(2\pi nk/N)$ ناپدید میشود.

فاکتور تغییر مقیاس در اینجا بوسیله مساحت مستطیل اول قابل محاسبه است. بنابراین،

مساحت زیر مستطیل: $N\nu = N\frac{F_s}{N}=F_s$

که برابر با همان مقداری است که در شکل 3 بدست آمد (بدون در نظر گرفتن $2\pi$ ). از آنجا که سیگنال متناوب است، شامل ضربه‌هایی است که در مضربهای صحیح $F_s$ تکرار میشوند – درست به همان ترتیب که در شکل 3 ملاحظه کردید ( به جز فاکتور $2\pi$ که اکنون در $F$ بررسی میکنیم). دنباله کامل بدست آمده در شکل 7 نشان داده شده است:

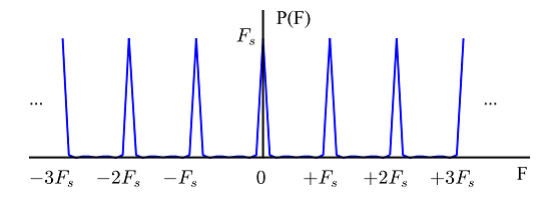
شکل 7- نمایش شاخه I از شکل 6 در محدوده $(-3F_s,+3F_s)$ برای $N$ بزرگ

در اینجا مساله را متوجه شدم. تمامی گرافها و شکلهایی که تاکنون رسم شده است و کتابهای درسی پردازش سیگنال نیز رسم کرده‌اند، از مقدار تغییر مقیاس غلط بر روی محور استفاده کرده‌اند. اگرچه دنباله‌های ضربه حوزه زمان و فرکانس خیلی مشابه یکدیگر هستند، اما در حقیقت مشابه نیستند. یک عدد خیلی بزرگ مثلا $L$ را فرض کنید. حال اگر نمایش قطار ضربه حوزه زمان یا فرکانس در محدوده $-L$ تا $+L$ را رسم کنیم، سیگنالها مشابه آنچه که در شکل 8 آمده است به نظر می‌آیند (در اینجا نرخ نمونه‌برداری 8 مگاهرتز است). همانطور که مشخص است، تمام ابهامی که در محور y وجود دارد ناشی از مقیاس ناصحیح محور x است.

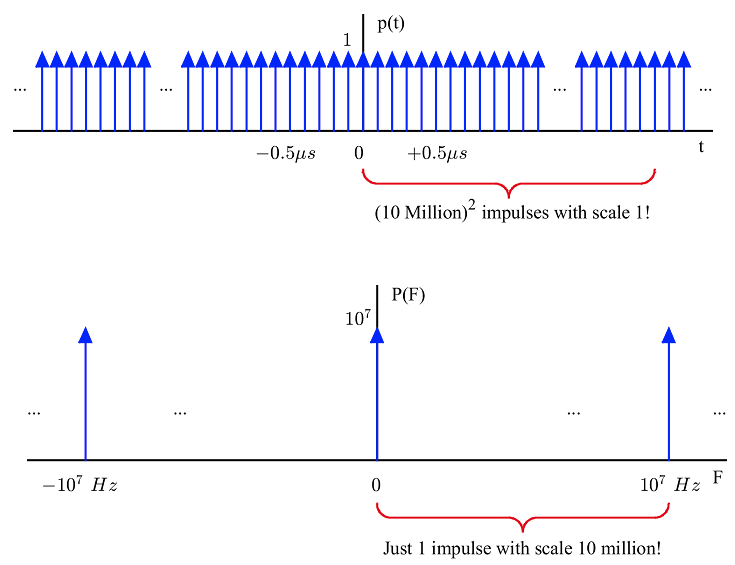
شکل 8- برای نرخ نمونه‌برداری 8 مگاهرتز، 10 میلیون ضربه در حوزه زمان فقط برای یک ضربه در حوزه فرکانس وجود دارد.

در اینجا ساده‌تر است که بگوییم که برای مبدل ADC که در فرکانس 10MHz کار میکند، به ازای فقط یک ضربه در حوزه فرکانس، 10 میلیون ضربه در حوزه زمان وجود دارد. اجازه دهید برابری انرژی در حوزه زمان و فرکانس را نیز از طریق دیگری (قاعده معروف پارسوال) نشان دهیم.

$\lim_{L\rightarrow \infty}\int_{-L}^{+L}\left | x(t) \right |^2dt = \lim_{L\rightarrow \infty}\int_{-L}^{+L}\left | X(F) \right |^2dF$

واضح است که تغییر مقیاس محور فرکانس با $F_s$ به نظر کاملا منطقی می‌آید. سیگنال باریک در حوزه زمان، در حوزه فرکانس وسیع خواهد بود. این مساله یادآور رسم ساختار یک اتم در کنار منظومه شمسی برای بررسی تشابه آنها است (شکل 9).

شکل 9- یک اتم و منظومه شمسی

این مساله، مفهوم استفاده از متغیر فرکانس $F$ به جای $\Omega$ را نیز توجیه میکند. در حالیکه $\Omega$ مزایای خود را دارد، متغیر $F$ ما را به چیزی که آن بیرون است متصل میکند: واقعیت. باند فرکانسی ISM معمولا $2.4 GHz$ است و نه $4.8\pi G-rad/s$

حرکت به فضای گسسته

اجازه دهید نتایج خود را در حوزه گسسته مطرح کنیم. در این رابطه دو نکته باید در نظر گرفته شود:

1- تفاوت اصلی بین ضربه زمان-پیوسته و ضربه زمان -گسسته آن است که ضربه گسسته در واقع دامنه واحد دارد و نیازی به تعریف مفهوم مساحت زیر منحنی ندارد.

2- فاکتور $N$ ای وجود دارد که در عبارتها وارد میشود که وابسته به نحوه تعریف تبدیلهای فوریه مختلف است. این مقدار، معادل فاکتور $2\pi$ برای حوزه فرکانس پیوسته $\omega$ در تبدیل فوریه زمان-گسسته است.

$x[n]=\frac{1}{2\pi}\int_{\omega=-\pi}^{+\pi}X(e^{j\omega})e^{j\omega n}d\omega, x[n]=\frac{1}{N}\sum_{k=-\frac{N}{2}}^{+\frac{N}{2}-1}X(k)e^{j2\pi \frac{k}{N}n}$

یک قطار ضربه گسسته $p[n]$ دنباله‌ای از ضربه‌های واحد است که با تناوب $M$ در پنجره مشاهده ما تکرار میشوند ( و همینطور خارج از این پنجره به دلیل متناوب بودن). شکل 10 آن را در حوزه زمان برای $N=15$ و $M=3$ نشان میدهد.

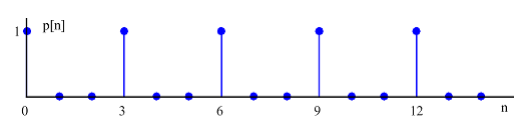
شکل 10- قطار ضربه گسسته در حوزه زمان برای $N=15$ و $M=3$

برای محاسبه تبدیل فوریه گسسته $N$ -نقطه‌ای آن $P[k]$ میتوان نوشت:

$P[k]=\sum_{n=0}^{N-1}p[n]e^{-j2\pi \frac{k}{N}n}=\sum_{m=0}^{N/M-1}1.e^{-j2\pi \frac{k}{N/M}m} \\ = \left\{\begin{matrix}\frac{1}{M}N & k=integer\times \frac{N}{M} \\ 0 & otherwise \end{matrix}\right.$

برخی نکات در مورد عبارت بالا به شرح زیر است:

تبدیل DFT با تاکید بر عبارت $\frac{k}{N}$ نوشته شده است زیرا این تبدیل به فرکانس زمان-پیوسته $\frac{F}{F_s}$ مربوط میشود و به طور صریح $n$ متغیر زمان است که مشابه $t$ در مدل زمان-پیوسته است ( $2\pi \frac{F}{F_s}n$ یا $2\pi ft$ را تصور کنید).
در رفتن از معادله اول به معادله دوم، از این حقیقت که $p[n]=0$ به جز زمانیکه $n=mM$ استفاده شده است.
معادله سوم مجدد از طرق مختلف قابل محاسبه است همچون روشی که در حالت زمان-پیوسته قبلا ارائه شد.

خروجی DFT نهایی در شکل 11 برای $N=15$ و $M=3$ آمده است.

شکل 11- قطار ضربه گسسته در حوزه فرکانس برای $N=15$ و $M=3$

دقت کنید که قطار ضربه حوزه زمان به چه شکل به قطار ضربه حوزه فرکانس در می‌آید. بنابراین برای $N=15$ و قطار ضربه زمان-گسسته با تناوب 3، تبدیل DFT نیز یک قطار ضربه با تناوب $\frac{N}{3}=5$ است. علاوه بر این، ضربه‌های واحد در حوزه فرکانس دارای دامنه $\frac{N}{3}=5$ هستند. قابل مشاهده است که تناوب کمتر M در حوزه زمان منجر به تناوب بیشتر N/M در حوزه فرکانس میشود. همچنین، دامنه ضربه‌های حوزه فرکانس N/M برابر بزرگتر هستند.

این مساله همان نتیجه بدست آمده برای حوزه فرکانس پیوسته با قطار ضربه با تناوب Fs و فاکتور تغییر مقیاس Fs است. هر چند که، در حوزه گسسته این موضوع بسیار واضح‌تر است زیرا تبدیل DFT با اندازه N یک سیگنال محدود است. این همان موضوعی است که دلیل محدود کردن فرکانس در حوزه پیوسته به بازه +-L برای یک مقدار بزرگ L است.

نمونه‌برداری در حوزه گسسته: کاهش نمونه‌ها

با توجه به مطالب بالا، میخواهیم بررسی کنیم که در حین نمونه‌برداری یک سیگنال زمان-گسسته با قطار ضربه زمان-گسسته چه اتفاقی رخ میدهد. به زبان پردازش سیگنال، این فرآیند تحت عنوان کاهش نمونه‌ها (downsampling) شناخته میشود. اگرچه خیلی مرسوم است که کاهش نمونه‌های سیگنال زمان-گسسته به عنوان فرآیند مستقل و جدا از نمونه برداری یک سیگنال زمان-پیوسته بحث شود، اما هر دو فرآیند به شدت به هم وابسته بوده و دید عمیق و مناسبی نسبت به هم ارائه میدهند.

یک سیگنال $x[n]$ با نگه داشتن هر نمونه $D$ ام و حذف بقیه نمونه‌ها، دچار کاهش نمونه با نرخ $D$ میشود. چنین فرآیندی میتواند به صورت ضرب سیگنال $x[n]$ در یک قطار ضربه $p[n]$ با دوره تناوب $D$ و دور ریختن نمونه‌های برابر با صفر میانی در نظر گرفته شود. در نتیجه، یک کانولوشن بین $X[k]$ و $P[k]$ و تعداد $D$ نسخه از طیف $X[k]$ انجام میشود: یک نسخه به ازای $k=0$ و مابقی به ازای مضارب صحیح $\pm integer\times \frac{N}{D}$ که همگی دامنه طیفی برابر با $\frac{N}{D}$ دارند. با افزایش $D$ نسخه‌های تکراری طیف فرکانسی به هم نزدیکتر شده و اندازه آنها متناسب با آن کاهش می‌یابد. این موضوع در شکل 12 برای کاهش نمونه‌ها با نرخ $D=3$ نشان داده شده است.

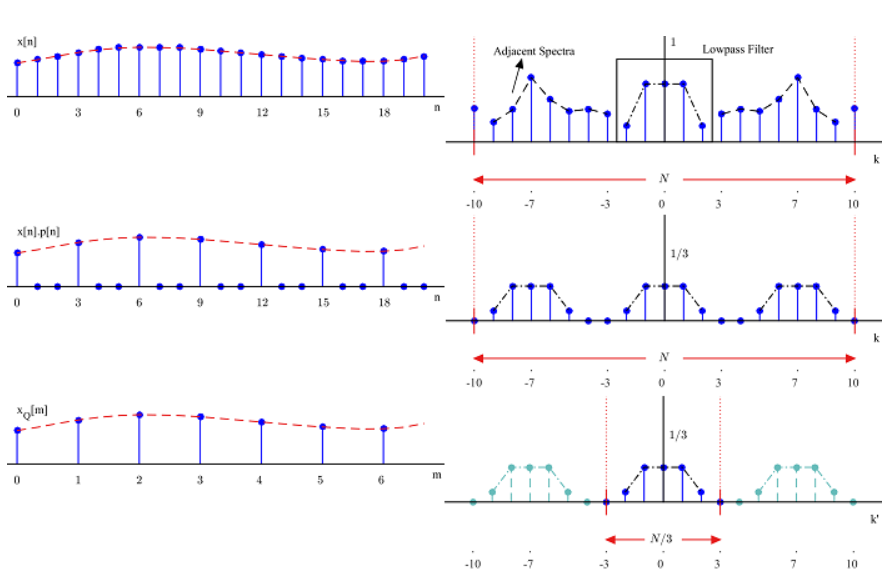
شکل 12- کاهش نمونه‌های سیگنال $x[n]$ با نرخ $D=3$ در حوزه زمان و فرکانس

این مساله دقیقا همان مفهومی است که در نمونه‌برداری سیگنال زمان-پیوسته وجود دارد. همچنان که با کاهش نرخ نمونه‌برداری، دامنه و گستره نسخه‌های تکراری طیف فرکانسی کاهش می‌یابد، دامنه و گستره نسخه‎های تکراری طیف با دور ریختن بیشتر نمونه‌ها در کاهش نرخ نمونه‌بردای نیز کم میشوند. در اولی این مساله با نسبت $\frac{1}{T_s}$ رخ میدهد و در دومی با نسبت $\frac{1}{D}$ .

به این شکل نیز میتوان گفت که نسبت $\frac{1}{D}$ یک نمونه از هر $D$ نمونه را انتخاب میکند. و $\frac{1}{T_s}$ یک نمونه از هر $T_s$ نمونه را. در اینجا $\frac{1}{T_s}$ تابع چگالی احتمال متغیر تصادفی با توزیع یکنواخت در محدوده $[0,T_s)$ است.

نگاه از زاویه‌ای دیگر

میتوان نگاه دیگری به مساله نمونه‌برداری نیز داشت. در ابتدا، ویژگی تغییر مقیاس تبدیل فوریه را در نظر بگیرید:

$x(a.t)\overset{F}{\rightarrow}\frac{1}{\left | a \right |}X(\frac{F}{a})$

سپس، به جای نمونه‌برداری ضربه‌ای، میتوان آن را به شکل تغییر مقیاس محور زمان در نظر گرفت. اگر مقدار ثابت $a$ را برابر با $T_s$ فرض کنیم:

$x(T_s.t)=x(tT_s)\overset{F}{\rightarrow}\frac{1}{T_s}X(F=\frac{f}{T_s})$

در اینجا، $x(tT_s)$ نسخه مشابه $x(nT_s)$ در نمونه‌برداری ضربه‌ای است با این تفاوت که عدد حقیقی $t$ به جای عدد صحیح $n$ استفاده شده است. همچنین، به جای مقیاس زمانی نانو یا میکروثانیه، $T_s$ واحد مشخصی ندارد و فقط آن را به این شکل در نظر میگیریم که در محدوده $[0,T_s)$ به بخشهای بینهایت کوچکی تقسیم شده است و $T_s$ تنها یک مقدار مثبت است. به این طریق، این مساله مشابه کاهش نرخ نمونه‌برداری با نرخ $D$ به ازای مقادیر همواره بزرگتر از یک میشود.

محور $x$ در نمودار طیف فرکانسی نیز با $T_s$ تغییر مقیاس داده میشود که منجر به رابطه اساسی بین فرکانس زمان-پیوسته $F$ و فرکانس زمان-گسسته $f$ میشود:

$f=F.T_s \rightarrow \omega=\Omega.T_s$

در این چهارچوب، تنها پس از حذف نمونه‌های میانی است که نسخه‌های تکرار شونده طیف فرکانسی ظاهر میشوند. این در نتیجه تعریف محور فرکانسی در رابطه با سیگنالهای متناوب است. البته ممکن است تعریف مشابه دیگری نیز برای فرکانس وجود داشته باشد که پردازش نمونه‌ها را ساده‌تر کند.

منبع: https://www.dsprelated.com

نکاتی درباره نمونه‌برداری سیگنال

دیدگاه ها (0)

لغو پاسخ