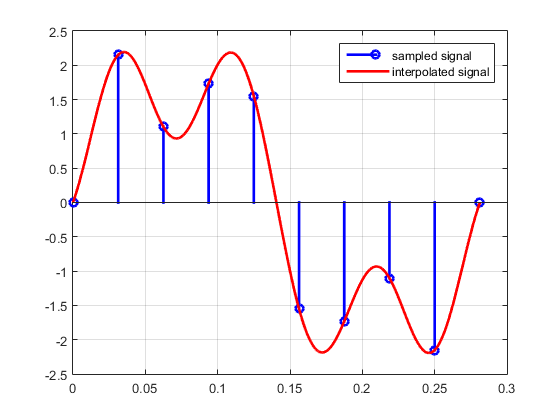
اصول درونیابی (Interpolation)
در این نوشتار اصول اولیه درونیابی به همراه مثال عددی از درونیابی یک سیگنال زمانی ارائه خواهد شد. شکل 1 آنچه را که ما درونیابی میدانیم، نشان میدهد. شکل بالایی یک سیگنال زمان پیوسته را نشان میدهد و شکل میانی شکل نسخه نمونهبرداری شده آن را با زمان نمونهبرداری نشان میدهد. هدف از درونیابی افزایش نرخ نمونهبردای تا جایی است که مقدار نمونههای درونیابی شده جدید به مقدار تابع زمان پیوسته در همان زمانها نزدیک باشد. برای مثال، اگر ما نرخ نمونهبرداری را 4 برابر کنیم، سیگنال درونیابی شده در شکل پایینی شکل 1 بدست میآید. زمان بین نمونهها از
به
کاهش پیدا کرده است.
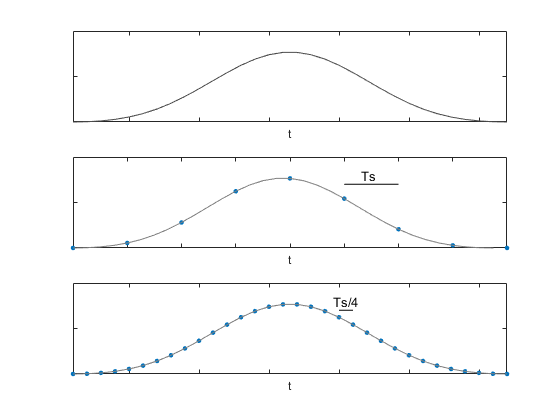
شکل 1- بالا: سیگنال پیوسته وسط: سیگنال با زمان نمونهبرداری پایین: سیگنال درونیابی شده با زمان نمونهبرداری
قبل از آنکه نحوه عملکرد درونیابی را شرح دهیم، بهتر است نگاهی به دو سیگنال نمونهبرداری شده و طیف فرکانسی آنها داشته باشیم. در ردیف بالایی شکل 2، سیگنال u با نرخ 400 هرتز نمونهبرداری شده است و اندازه طیف فرکانسی آن در سمت راست نشان داده شده است. در ردیف پایین، سیگنال x متشکل از یک چهارم نمونههای سیگنال u است و بنابراین نرخ نمونهبرداری آن 100 هرتز است. مجدد طیف فرکانسی در سمت راست دیده میشود که در آن تصویر متقارن طیف به صورت خطچین نشان داده شده است. دقت کنید که اندازه طیف سیگنال یک چهارم سیگنال اولی است.
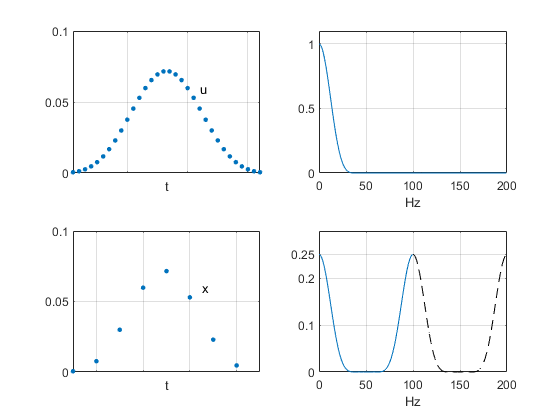
شکل 2- بالا: سیگنال نمونهبرداری شده با فرکانس و طیف فرکانسی آن (مقیاس خطی)
پایین: سیگنال نمونهبرداری شده با و طیف آن
حال بیایید نگاهی به مثال درونیابی با فاکتور صحیح 4 داشته باشیم. برای سیگنال که در بالا توضیح داده شد، درونیابی با فاکتور 4 منجر به سیگنال
میشود. کد متلب این مثال درونیابی در پایان همین نوشتار ارائه شده است.
اگر ما نرخ نمونهبرداری را خیلی ساده از 100 به 400 افزایش دهیم، شکل 3 حاصل میشود. در اینجا بین هر دو نمونه از سیگنال ، سه نمونه با مقدار صفر وارد میشود. فرآیندی که آن را با عنوان افزایش نمونهافزایی (upsampling) میشناسیم. نمونهافزایی شامل تغییر مقیاس اندازه دامنه سیگنال با نسبت 4 میشود که حداکثر اندازه طیف فرکانسی را به جای ¼ ، برابر با 1 میکند. طیف فرکانسی سیگنال نمونهافزا شده
در سمت راست نشان داده شده است. از آنجاییکه فاصله بین نمونههای سیگنال
برابر با فاصله نمونههای
از هم است، طیف فرکانسی آن نیز مشابه طیف
است به جز اندازه دامنه آن که با 4 برابر بزرگتر است.
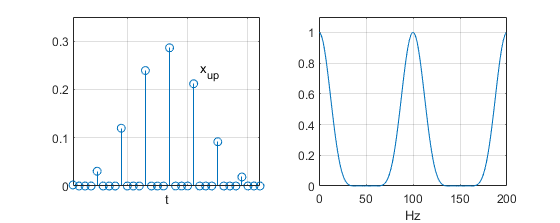
شکل 3- سیگنال نمونهافزا شده با فرکانس
و طیف فرکانسی آن در مقایس خطی
حال، اگر طیف فرکانسی با طیف
مقایسه شود، ملاحظه میکنیم که از فرکانس 0 تا 50 هرتز یکسان هستند ولی
طیفهای تکراری تصویر شده با فرکانسهای مرکزی 100 و 200 هرتز دارد. بنابراین، به نظر میرسد که میتوانیم سیگنال
را با فیلتر کردن سیگنال
با یک فیلتر پایینگذر برای حذف تصاویر طیفی اضافی بدست آوریم. اگر این ترفند درست عمل کند، سیگنال درونیابی شده
با فاکتور 4 را خواهیم داشت. یک بلوک دیاگرام سیستم درونیاب در شکل 4 نشان داده شده است. در مثال ما L=4 است.
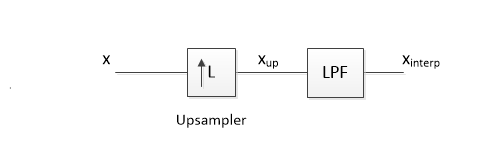
شکل 4- بلوک دیاگرام سیستم درونیاب
برای طراحی فیلتر پایینگذر، طیف فرکانسی را در مقیاس لگاریتمی همانطور که در بخش بالایی شکل 5 نشان داده شده است، در نظر خواهیم گرفت. نیاز به فیلتری داریم که بخش طیف فرکانسی مطلوب را از خود عبور داده و تصاویر طیفی نامطلوب را تضعیف کند. بنابراین، محدودههای باند عبور و توقف زیر را داریم:
باند عبور: 0 تا 36 هرتز
باند توقف: 66 تا 135 هرتز و 166 تا 200 هرتز
محدودههای 50 تا 66 هرتز و 135 تا 166 هرتز را نامشخص میگذاریم زیرا اندازه دامنه طیف در این نواحی بسیار کم است. کد متلب ارائه شده در بخش انتهایی شامل فیلتر درونیابی از نوع با پاسخ ضربه محدود (FIR) از مرتبه 41 میشود. پاسخ فیلتر در بخش میانی شکل 5 آمده است. طیف سیگنال درونیابی شده
نیز در بخش پایینی نشان داده شده است.
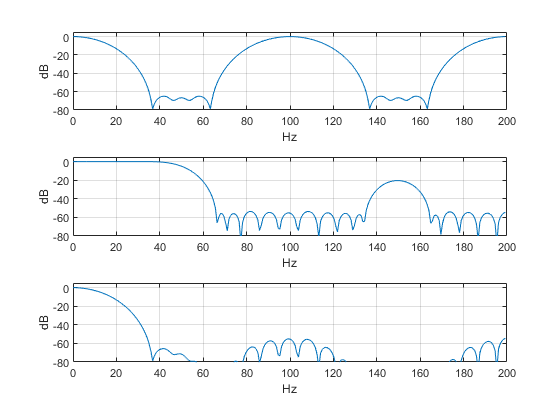
شکل 5- بالا: طیف سیگنال
وسط: پاسخ فیلتر پایینگذر درونیاب
پایین: طیف سیگنال
سیگنال در سمت چپ شکل 6 و طیف آن در مقیاس خطی در سمت راست نشان داده شده است. خوشبختانه، سیگنال
مشابه سیگنال
در شکل 2 است.
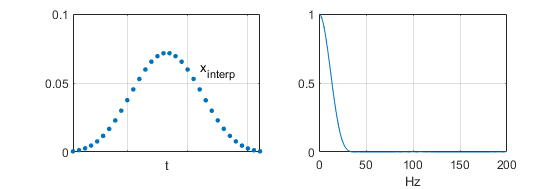
شکل 6- سیگنال درونیابی شده در سمت چپ و طیف فرکانسی آن با مقیاس خطی در سمت راست.
ما میتوانیم خطای بین دو سیگنال را بوسیله فرمول زیر محاسبه کنیم:
خطا در شکل 7 رسم شده است. با توجه به چگونگی دستیابی به این نتیجه، لازم به ذکر است که عمل درونیابی سیگنال در حوزه زمان با علم به طیف فرکانسی سیگنال ورودی انجام شده است.
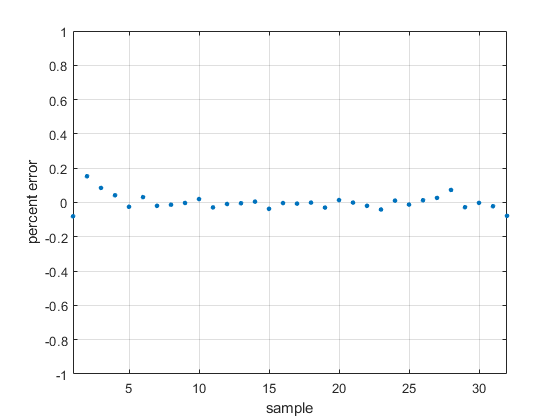
شکل 7- درصد خطای درونیابی
کد متلب درونیابی با فاکتور 4
در کد متلب پیش رو سیگنالها با همان نامهایی که در متن اشاره شدند، نامگذاری شدهاند.
سیگنال نمونهبرداری شده با فرکانس 400 هرتز
سیگنال ورودی به سیستم درونیاب با فرکانس نمونهبرداری 100 هرتز
نسخه نمونهافزا شده
با فرکانس نمونهبرداری 400 هرتز
خروجی فیلتر درونیاب با فرکانس نمونهبرداری 400 هرتز
سیگنال یک تابع پنجره چبیشف (Chebyshev window function) با طول 32 و لوبهای جانبی -70 دسیبل است. توابع دیگر نیز قابل استفاده هستند همچون پنجره بلکمن (Blackman window). همانطور که قبلا اشاره شد، محاسبه
شامل تغییر مقیاس با نرخ 4 میشود. خروجی سیستم درونیاب طولی برابر با 72 خواهد داشت. نمونههای 21 تا 52 برای تقریب سیگنال u استفاده میشوند.
فرکانس نمونهبرداری فیلتر درونیاب برابر با 400 هرتز است و توسط الگوریتم پارکس-مککللان (Parks-McClellan) در متلب و توسط تابع firpm شبیهسازی شده است. ضرایب فیلتر طراحی شده در شکل 8 نشان داده شده است و پاسخ فرکانسی فیلتر نیز در بخش میانی شکل 5 آمده است.
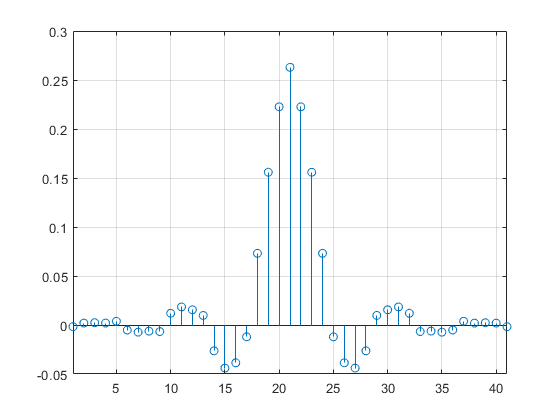
شکل 8- ضرایب فیلتر درونیاب با فاکتور 4
دقت کنید با اینکه روند طراحی بسیار مشخص و سرراست است، نتیجه منجر به یک درونیاب با راندمان حداکثر نمیشود. رویکرد جایگزین دیگر، استفاده از دو درونیاب سری شده است که در شکل 9 نشان داده شده است. با این روش امکان استفاده از فیلترهای درونیاب نیمباند وجود خواهد داشت که البته برای مطالعه بیشتر مرجع زیر پیشنهاد میشود.
Harriz, Fredric, J. Multirate Signal Processing for Communication Systems, Prentice Hall, 2004, Chapter 7
کد متلب:
% interp_demo.m 8/17/2019 Neil Robertson
% Demonstrate interpolation by 4
fs= 400; % Hz sample rate
p= chebwin(32,70)’; % signal = Chebyshev window
u= p/sum(p); % normalize for sum = 1
x= [u(1:4:end)]; % interpolator input signal, fs= 100
% upsampling
x_up= zeros(1,32);
x_up(1:4:32)= 4*x(1:8); % upsampled signal
% interpolation filter using Parks-McClellan algorithm
fn= fs/2;
f= [0 36 66 135 166 199]/fn; % frequency vector
a= [1 1 0 0 0 0]; % amplitude goal vector
Ntaps= 41;
b= firpm(Ntaps-1,f,a); % synthesize filter coeffs
b= round(b*2^13)/2^13; % fixed point coeffs
%
x_interp= conv(x_up,b); % filter x_up
interp_error= 100*(x_interp(21:52) – u)/max(u);
%
[Xup,f]= freqz(x_up,1,256,fs); % spectrum of x_up
Xinterp= freqz(x_interp,1,256,fs); % spectrum of x_interp
%
%
% plotting
subplot(211),plot(u,‘.’,‘markersize’,10),grid
axis([1 32 0 .1]),xticklabels({}),text(23,.06,‘u’)
subplot(212),plot(x,‘.’,‘markersize’,10),grid
axis([1 9 0 .1]),xticklabels({}),text(6.5,.06,‘x’),figure
stem(b),grid
axis([1 41 -.05 .3]),title(‘Interpolation Filter Coefficients b’)
figure
subplot(211),stem(x_up),grid
axis([1 32 0 .35]),xticklabels({}),text(23,.24,‘x_{up}’)
subplot(212),plot(x_interp(21:52),‘.’,‘markersize’,10),grid
axis([1 32 0 .1]),xticklabels({}),text(23,.06,‘x_{interp}’),figure
plot(interp_error,‘.’,‘markersize’,10),grid
axis([1 32 -1 1]),xlabel(‘sample’),ylabel(‘percent error’)
title(‘Interpolation Percent Error’),figure
subplot(211),plot(f,abs(Xup)),grid
xlabel(‘Hz’)
axis([0 fs/2 0 1]),title(‘Spectrum of x_{up} (linear amplitude scale)’)
subplot(212),plot(f,abs(Xinterp)),grid
xlabel(‘Hz’)
axis([0 fs/2 0 1]),title(‘Spectrum of x_{interp} (linear amplitude scale)’)
منبع: www.dsprelated.com

دیدگاه ها (0)