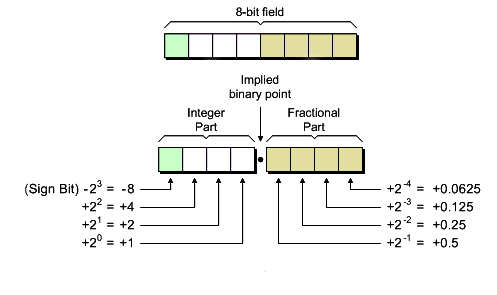
آشنایی با نمایش نقطه‌ثابت (fixed-point)

نمایش محدود اعداد اعشاری تحت عنوان نقطه‌ثابت یا fixed-point شناخته میشود. نقطه‌ثابت یک تفسیر از اعداد مبتنی بر پایه 2 است که معمولا دارای علامت هستند ولی به نمایش با علامت محدود نمیشوند. این روش ابزار ما را از نمایش طول محدود اعداد به شکل صحیح به اعداد با اجزاء اعشاری توسعه میدهد. نمایش نقطه‌ثابت از یک عدد شامل بخش صحیح و اعشاری آن میشود. طول بیت در این نمایش به شکل زیر تعریف میشود:

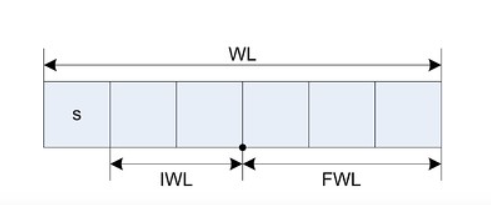
$X_{Nbits}=X_{IntegerNbits}+X_{FractionNbits}+1$

شکل 1- بخشهای مختلف نمایش نقطه‌ثابت

در اینجا IWL طول بخش صحیح، FWL طول بخش اعشاری و WL طول کل عدد است. برای نمایش نقطه‌ثابت مبتنی بر پایه 2 داریم:

$WL=1+IWL+FWL$

از طریق این نمایش، محدوده اعداد برابر با $[-2^{IWL},2^{IWL})$ است و اندازه گام (رزولوشن) برابر با $2^{-FWL}$ است. عدد نقطه‌ثابت به فرمت (wl,iwl,fwl) یا ویژگیهای دامنه، رزولوشن و بایاس تعریف میشود. همانطور که گفته شد، یک عدد نقطه‌ثابت به جای اینکه با تعداد بیتهای خود تعریف شود، بوسیله دامنه و رزولوشن خود مشخص میگردد. برای طراحی یک سیستم نقطه‌ثابت، منطقی است که بر اساس نیاز دامنه و رزولوشن مورد نظر عمل شود و به صورت الگوریتمی تعداد بیتها در زمان طراحی سیستم مشخص شوند. به عبارت دیگر، در فاز طراحی، با دامنه و رزولوشن شروع میشود و در مرحله پیاده‌سازی تعداد بیت مورد نیاز مشخص میگردد.

معمولا، برای فرمت نقطه‌ثابت از یک ساختار ساده و کوتاه استفاده میشود. فرمت Q در پردازشگرهای نقطه‌ثابت مرسوم است. البته در اینجا از این فرمت استفاده نمیشود زیرا چندان منعطف نیست و با توجه به نمونه‌های قدیمی‌تر پردازشگرهای نقطه‌ثابت، ابهام‌آمیز خواهد بود. در اینجا به طور صریح از نماد W=(wl,iwl,fwl) استفاده میشود. این نماد، تعداد بیتهای بخش صحیح، اعشاری و طول بیت کل را تعریف میکند. مثلا، W=(4,0,3) یک عدد 4 بیتی با 3 بیت اعشاری و یک بیت علامت است (بیت علامت به طور ضمنی است). تمامی اعداد نقطه‌ثابت در این مقاله به شکل نمایش مبتنی بر پایه 2 هستند.

چرا از اعداد نقطه‌ثابت استفاده کنیم؟

چرا از این نمایش اعداد باید بهره برد؟ چرا تمامی مقادیر را به یک دامنه صحیح نرمالیزه نکنیم و تنها با اعداد صحیح کار نکنیم؟ بر اساس نقطه نظر شما ممکن است این موضوع واضح باشد یا نباشد. بسیاری از طراحان ترجیح میدهند که تمامی مقادیر را به اعداد صحیح نرمالیزه کنند اما این کار باعث غیر‌قابل خواندن کدها و مستندسازی‌های مرتبط با آنها میشود. نمایش نقطه‌ثابت برای راحتی بیشتر در کار با اعداد استفاده میشود (مشابه استفاده از exp jw). به طور مثال، اگر به کد منبع زیر نگاهی داشته باشیم:

c0 = fixbv(0.0032, min=-1, max=1, res=2**-15)
c1 = fixbv(-0.012, min=-1, max=1, res=2**-15)

میتوان به سادگی این مقادیر را تفسیر کرد ولی در کد زیر:

c0 = intbv(0x0069, min=-2**15, max=2**15)
c1 = intbv(-0x0189, min=-2**15, max=2**15)

اطلاعات اضافی نیاز است. این نمایش به شکل اعداد صحیح نرمالیزه شده، به سختی قابل درک است. علاوه بر مزایای نمایش نقطه‌ثابت، ابزار مورد نیاز برای حل مشکلاتی همچون گرد شدن اعداد و سرریز (overflow) برای نمایش نقطه‌ثابت طراحی شده‌اند.

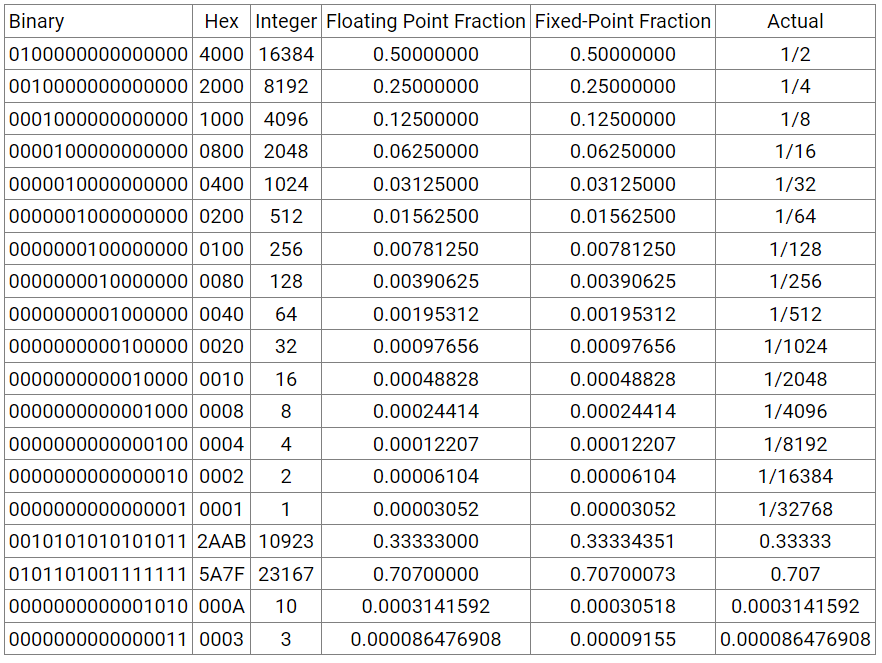
حال که تعاریف اصلی نقطه‌ثابت باینری ارائه شد، بهتر است که نگاهی به برخی مقادیر اعشاری که به فرمت نقطه‌ثابت تبدیل شده‌اند، داشته باشیم. جدول 1 مثالی از نمایش نقطه‌ثابت است:

جدول 1- مثالهای نقطه‌ثابت

مثلا یک عدد اعشاری با علامت، به شکل زیر نوشته میشود:

     b7    b6    b5    b4    b3     b2    b1    b0  
     S     F     F     F     F      F     F     F
     0     1     0     1     1      0     0     1
   +-1    1/2   1/4   1/8   1/16   1/32  1/64  1/128

که مقدار اعشاری تا 4 بیت به صورت زیر محاسبه میشود:

Value = + 1/2 + 1/8 + 1/16 + 1/128 which equals
        = + 0.5 + 0.125 + 0.0625 + 0.0078125
        = 0.6953125

به عنوان مثالی دیگر، فرض کنیم عدد 26.5 را میخواهیم نمایش دهیم. در نمایش دهدهی داریم:

2 * 10¹ + 6 * 10⁰ + 5 * 10^-1= 26.5

اما در نمایش نقطه‌ثابت باینری، ضریب وزنی اعداد در بخش صحیح به شکل $2^0,2^1,2^2$ است و در بخش اعشاری به شکل $2^{-1},2^{-2},2^{-3}$ است. مثلا برای عدد 26.5 داریم:

11010.1₂

= 1 * 2⁴ + 1 * 2³ + 0 * 2² + 1 * 2¹ + 0* 2⁰ + 1 * 2^-1

= 16 + 8 + 2 + 0.5

= 26.5

در اینجا نمایش نقطه‌ثابت عدد 26.5 برابر با 11010.1 است. شکل زیر این نمایش را نشان میدهد:

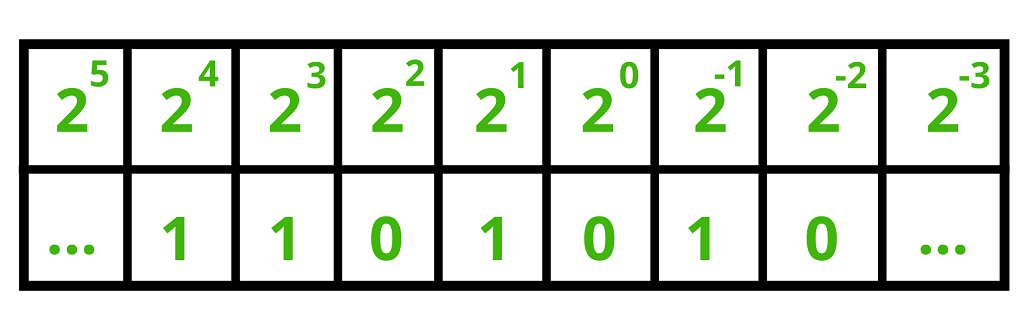
شکل 2- نمایش نقطه‌ثابت عدد 26.5

با توجه به مثالهای بالا میتوان نحوه نمایش مقادیر اعشاری و صحیح در نمایش نقطه‌ثابت را مشخص کرد. به طور کلی میتوان فرمول زیر را برای نمایش نقطه‌ثابت در نظر گرفت با فرض اینکه بردارهای بخش صحیح و اعشاری باینری به طور مجزا وجود داشته باشند:

$\sum_{k=0}^{IWL-1}b_I[k]2^k+\sum_{k=0}^{FWL-1}b_F[k]2^{-(k+1)}$

در فرمول بالا فرض بر این است که با افزایش اندیس بیت، موقعیت آن در مقادیر بالاتر قرار میگیرد.

الگوی جابه‌جایی (shift)

در یک سیستم باینری با جابه‌جایی یک رقم به راست، عمل تقسیم بر دو انجام میشود و به سمت چپ ضرب در عدد دو انجام میشود.

نمایش بدون علامت

در اینجا تمامی بیتهای سمت چپ نقطه باینری برای بخش صحیح قابل استفاده است. به طور مثال داریم:

00010.1102
= 1 * 2¹ + 1 * 2^-1 + 1 * 2^-2

= 2 + 0.5 + 0.25

= 2.75

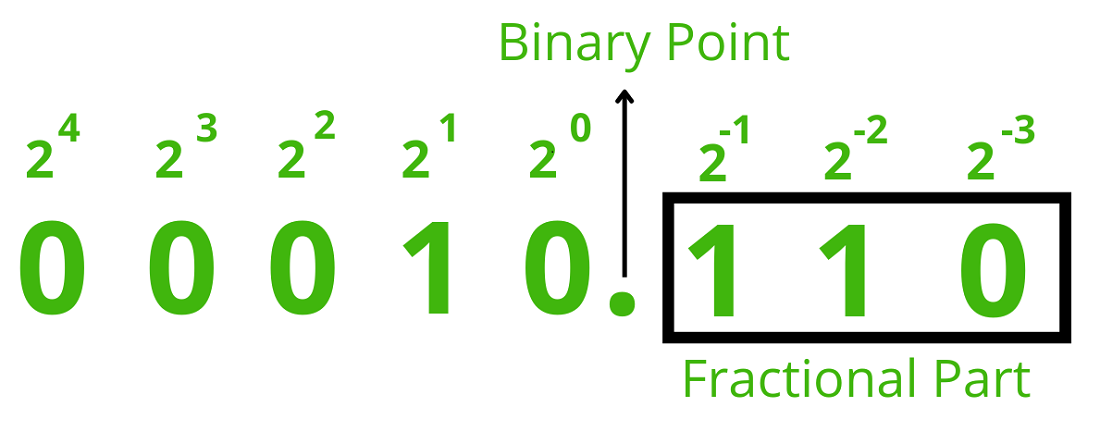
شکل 3- بخشهای صحیح و اعشاری در نمایش بدون علامت نقطه‌ثابت

نمایش با علامت

اعداد منفی در سیستم عددی باینری با استفاده از نمایش اعداد با علامت نشان داده میشوند. اگرچه در ریاضیات از علامت “-” برای این کار استفاده میشود ولی در نمایش نقطه‌ثابت باید از بیتها برای این کار استفاده کرد. اعداد باینری با علامت به یکی از سه روش زیر قابل نمایش است:

1- فرم علامت-اندازه ( $sign-magnitude$ )

2- فرم مکمل 1 ( $1's \ complement$ )

3- فرم مکمل 2 ( $2's \ complement$ )

فرم علامت-اندازه

در این روش، علامت عدد به صورت با ارزشترین بیت یا سمت چپ‌ترین بیت (MSB) نمایش داده میشود و مابقی بیتها اندازه عدد را نشان میدهد. مثلا برای یک عدد 8 بیتی داریم:

55 ₁₀ = 00110111₂

−55 ₁₀ = 10110111₂

فرم مکمل 1

با مکمل کردن هر بیت از یک عدد باینری، نمونه مکمل 1 آن بدست می‌آید. انجام این عمل روی یک عدد باینری در این فرم منجر به عدد مورد نظر با علامت مخالف میشود. به عبارت دیگر عدد مثبت، منفی شده و منفی، مثبت میشود:

55 ₁₀ = 00110111₂

−55 ₁₀ = 11001000₂

فرم مکمل 2

با اضافه کردن عدد یک به فرم مکمل 1 یک عدد باینری، فرم مکمل 2 آن بدست می‌آید. در اینجا هم مکمل 2 تغییر علامت ایجاد میکند:

55 ₁₀ = 00110111₂

−55 ₁₀ = 1+11001000₂+11001001₂

یا مثلا برای عدد اعشاری زیر داریم:

2.5 ₁₀ = 0101 ₂

-2.5 ₁₀ = 1010 ₂ + 1 (1’s complement + 1 = 2’s complement)

-2.5 ₁₀ = 1011 ₂

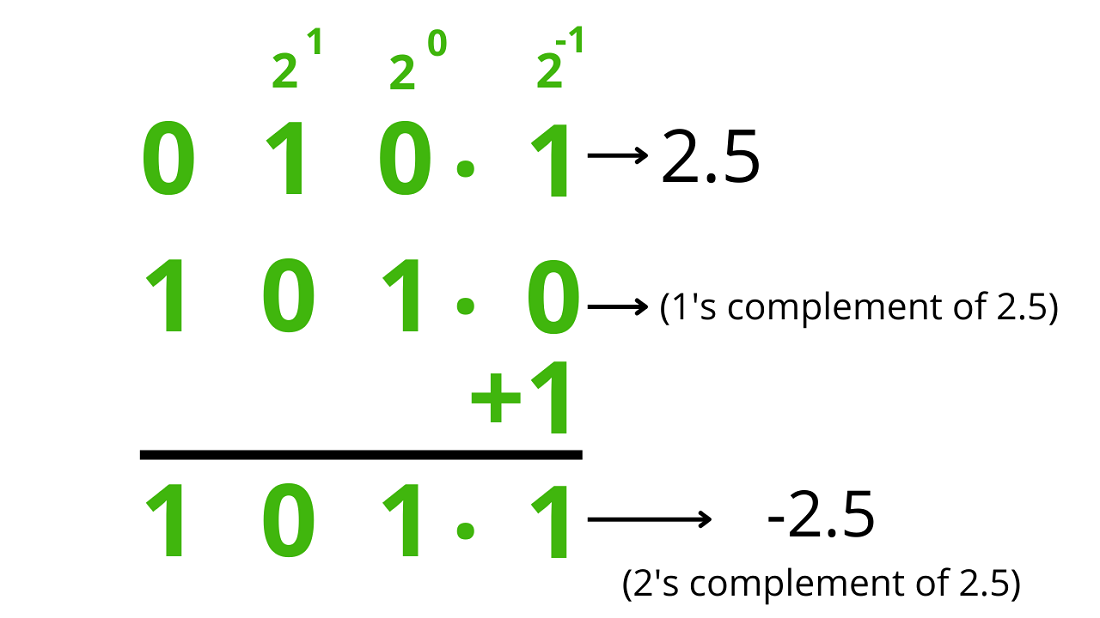
شکل 4- عدد 2.5- در نمایش نقطه‌ثابت

ضرب و جمع در نمایش نقطه‌ثابت

در ادامه مثالهایی از ضرب و جمع آورده میشود. تفاضل در نمایش نقطه‌ثابت مشابه تفاضل مکمل 2 است (جمع با مقدار منفی).

ضرب

ضرب نقطه‌ثابت مشابه ضرب مکمل 2 است اما نیازمند تعیین مکان نقطه باینری بعد از ضرب است تا نتیجه کار درست بدست آید. مشخص کردن این نقطه، یک کار مهم در طراحی سیستم نقطه‌ثابت است. مثال زیر

ضرب 6.5625 در 4.25 است:

$6.5625 (W=(8,3,4))\times4.25(W=(8,5,2))$

0110.1001  == 6.5625
000100.01  == 4.25
          01101001  
        x 00010001  
      ------------
          01101001
         00000000 
        00000000  
       00000000  
      01101001    
     00000000      
    00000000
   00000000 
 --------------------
  x000011011111001   ==  0000011011.111001  ==  27.890625

تعداد بیتهای مورد نیاز برای نتیجه ضرب برابر است با جمع WL دو عدد ( $WL_{multiplicand}+WL_{multiplier}$ ). تغییر اندازه نتیجه ضرب (و جمع) کاملا عادی است و تعداد بیتها باید کاهش یابند. در نمایش نقطه‌ثابت، این مساله ملموس است زیرا بیتهای کوچکتر بخش اعشاری دور ریخته میشوند و مقدار عددی بر اساس این بیتهای حذف شده، رند میشود.

جمع

جمع کمی پیچیده‌تر است زیرا نقاط باینری باید قبل از انجام عمل جمع در یک راستا قرار گیرند. همان اعداد مثال ضرب در اینجا در نظر گرفته شده‌اند:

0110.1001  == 6.5625
000100.01  == 4.25
            0110.1001  
        + 000100.01  
        -------------
          001010.1101  ==  10.8125

برای جمع (یا تفریق) دو عدد یک بیت اضافی لازم است. زمانیکه بیش از دو عدد با هم جمع میشوند، اگر طول WL آنها یکسان باشد، تعداد بیتهای اضافی لازم برای نتیجه برابر با WL+log2(N) است که N تعداد اعدادی است که با هم جمع میشوند.

نمایش نقطه‌ثابت در مواجه با پیاده‌سازی الگوریتمها و محاسبات مختلف بسیار کارآمد و مفید است زیرا امکان انجام اینگونه محاسبات را برای اعداد اعشاری با علامت توسط سیستمهای کامپیوتری باینری فراهم می‌آورد.

آشنایی با نمایش نقطه‌ثابت (fixed-point)

دیدگاه ها (0)

لغو پاسخ