
آشنایی با فیلترها: فیلتر FIR در مقابل IIR
فیلترها، کاربردهای متعددی در جمعآوری داده (data acquisition) و تحلیل داده (data analysis) دارند. آنها برای تغییر محتوای فرکانسی یک سیگنال حوزه زمان از طریق تضعیف یا تقویت فرکانسهای مشخص، به کار میروند.
برای مثال، همانطور که در شکل یک نشان داده شده است، یک فیلتر پایینگذر (lowpass)، بر روی محتوای فرکانسی یک سیگنال حوزه زمان به سه روش مختلف، تاثیر میگذارد: بخشی از محتوای فرکانسی بدون تغییر میماند، در حالیکه سایر بخشهای محتوای فرکانسی به لحاظ دامنه سیگنال حوزه فرکانس، تضعیف شده و یا به کلی از سیگنال حذف میشوند.

شکل ۱- یک فیلتر پایینگذر، فرکانسهای پایین را بدون تغییر از خود عبور میدهد (چپ) و فرکانسهای بالا را حذف میکند (راست).
فیلترها علاوه بر تضعیف یا حذف فرکانسها، میتوانند محتوای فرکانسی را تقویت کنند. مقداری که یک فیلتر، دامنه یک سیگنال را میتواند تنظیم کند، قابل بیان به صورت مقیاس خطی (فاکتور تقویت) یا مقیاس دسیبل (dB) از تقویت/تضعیف مطابق شکل ۲ است.

شکل ۲- نمودار چپ: دامنه فیلتر در مقیاس خطی از فاکتور تقویت بر حسب فرکانس، نمودار راست: همان فیلتر در مقیاس دسیبل از تضعیف بر حسب فرکانس
مقیاس خطی، دارای برابریهای معادل زیر در مقیاس دسیبل است:
– نصف کردن دامنه در مقیاس خطی برابر با ۶ دسیبل تضعیف است.
– عدم تغییر دامنه معادل با بهره خطی واحد یا بهره دسیبل صفر است.
اگرچه، نمایش خصوصیات فیلترها در حوزه فرکانس مطلوب است، فیلترها کارشان را در حوزه زمان انجام میدهند (شکل ۳)

شکل ۳- یک سیگنال ورودی با نویز فرکانس بالا از یک فیلتر پایینگذر عبور میکند. خروجی حاصل، بدون نویز فرکانس بالا است که منجر به سیگنال تمیز و بدون نویز میشود.
یک فیلتر، سیگنال حوزه زمان را به عنوان ورودی دریافت میکند، محتوای فرکانسی را اصلاح میکند و یک سیگنال حوزه زمان جدید را به عنوان خروجی تحویل میدهد. این عمل برای بسیاری از کاربردها، مفید است.
۱- کاربردهای فیلترها
فیلترها به طرق مختلف استفاده میشوند، از حذف نویز از سیگنال و تمیز کردن آن تا تحلیل سیگنال. در برخی از کاربردها، فیلترها برای شرطگذاری روی یک سیگنال حوزه زمان با تضعیف محتوای فرکانسی نامطلوب به کار میروند. مثالها شامل موارد زیر میشود:
– فیلتر ضد الیاسینگ (anti-aliasing): یک فیلتر ضد الیاسینگ برای محتوای سیگنال که به شکل صحیح قابل دیجیتال کردن نیست، درست قبل از مبدل آنالوگ به دیجیتال (A/D) به کار میرود.
– حذف نویز: فیلترها میتوانند نویز فرکانس بالای ناخواسته را از یک سیگنال حذف کنند، برای مثال، یک صدای هیس در ضبط موسیقی.
– حذف رانش (drift): رانش یا جابهجایی زیاد در سیگنال، از طریق یک فیلتر بالاگذر یا کوپلینگ AC قابل حذف است.
برخی اوقات، فیلترها برای اعمال تغییرات خاصی بر روی سیگنال ورودی به منظور تحلیل آن، به کار میروند:
– وزندهی A: یک فیلتر وزندهی A (شکل ۴)، بر روی داده میکروفن برای اعمال ویژگیهای شنیداری انسان بر روی ضبط میکروفن، استفاده میشود. یک میکروفن، تمام فرکانسها را به طور یکسان دریافت میکند اما گوش انسان چنین کاری را انجام نمیدهد. فیلتر وزندهی A، بخشهای پایین و بالای فرکانسی سیگنال میکروفن را تضعیف میکند تا نحوه درک گوش انسان از صدا را به آن تحمیل کند.

شکل ۴- فیلتر وزندهی A در حوزه فرکانس. محور Y بهره یا تضعیف در مقیاس دسیبل است و محور X بر حسب فرکانس.
– ارتعاش بدن انسان: بدن انسان نسبت به فرکانسهای ارتعاشی خاصی حساستر از سایر فرکانسها است. یک فیلتر (تحت استاندارد ایزو ۲۶۳۱) را میتوان به منظور ارزیابی سلامت بدن انسان و میزان راحتی آن بر پایه سیگنال ارتعاش شتابسنج، استفاده کرد.
فیلترها به دو شکل سیستم آنالوگ (برای سیگنال زنده) و یا دیجیتال (برای اعمال روی سیگنال ضبط شده روی رایانه) قابل پیادهسازی هستند.
۲- انواع فیلتر
فیلترها را میتوان برای انجام کارهای مختلف طراحی کرد. برای مثال، یک فیلتر میتواند بالاگذر (highpass)، پایینگذر (lowpass)، میاننگذر (bandstop) یا میانگذر (bandpass) باشد (شکل ۵).

شکل ۵- انواع فیلترها
انواع فیلترها:
– بالاگذر: فیلتر بالاگذر برای حذف فرکانسهای پایین از یک سیگنال، استفاده میشود. برای مثال، اگر تنها به محتوای پویای سیگنال اندازهگیری کشش علاقمند هستیم، هر گونه فرکانس پایین در آن توسط یک فیلتر بالاگذر قابل حذف است.
– پایینگذر: یک فیلتر پایینگذر، فرکانسهای بالاتر از یک فرکانس خاص را حذف یا تضعیف میکند. برای مثال، این فیلتر برای حذف فرکانس بالا در بخش هیس در ضبط صدا قابل استفاده است.
– میانگذر: این فیلتر به منظور عبور یک باند فرکانس محدود از درون آن استفاده میشود.
– میاننگذر: یک فیلتر میاننگذر برای حذف فرکانسهای فراتر یک محدوده مشخص، استفاده میشود.
این انواع فیلتر به شکل فیلتر با پاسخ ضربه با طول محدود (Finite Impulse Response – FIR) یا فیلتر با پاسخ ضربه با طول نامحدود (Infinite Impuse Response) قابل پیادهسازی است. همچنین، امکان استفاده از ترکیب آنها برای تولید فیلتر با شکل خاص نیز وجود دارد.
۳- فیلتر FIR در مقابل IIR
دو کلاس از فیلترهای دیجیتال شامل FIR و IIR میشوند. عبارت ” پاسخ ضربه ” به شکل ظاهری فیلتر در حوزه زمان اشاره دارد. فیلترها نوعاً دارای پاسخهای فرکانسی وسیع هستند که متناظر با پالسهای زمان-کوتاه در حوزه زمان آنها میشود، مطابق شکل ۶.

شکل ۶- نمایش حوزه فرکانس (چپ) و حوزه زمان (راست) شکل فیلتر
معادلات هر دو نوع فیلتر FIR و IIR در زیر آمده است. وروی فیلتر سیگنال ![]() است و خروجی آن، سری زمانی
است و خروجی آن، سری زمانی ![]() . اولین نمونه سیگنال در حوزه زمان در
. اولین نمونه سیگنال در حوزه زمان در ![]() قرار دارد.
قرار دارد.

تفاوت ریاضی در پیادهسازی دو فیلتر FIR و IIR آن است که فیلتر IIR از بخشی از خروجی به عنوان ورودی استفاده میکند. این عمل باعث میشود که فیلتر IIR به شکل یک تابع بازگشتی (recursive) عمل کند.
هر معادله سه سری از اعداد را شامل میشود: یک گذشته زمانی به عنوان ورودی، یک فیلتر و یک گذشته زمانی خروجی (شکل ۷)

شکل ۷- سریهای زمانی ورودی، ![]() ، فیلتر FIR، سری
، فیلتر FIR، سری ![]() ، و خروجی،
، و خروجی، ![]() .
.
این سریها عبارت است از:
– سری ![]() : ورودی گذشته زمانی
: ورودی گذشته زمانی ![]() شامل نمونههای
شامل نمونههای ![]() ،
، ![]() تا
تا ![]() میشود. عدد n، تعداد کل نقطههای داده در گذشته زمانی سیگنال ورودی است.
میشود. عدد n، تعداد کل نقطههای داده در گذشته زمانی سیگنال ورودی است.
– سری ![]() : فیلتر توسط سری برچسبگذاری شده
: فیلتر توسط سری برچسبگذاری شده ![]() برای فیلتر FIR و
برای فیلتر FIR و ![]() و
و ![]() برای فیلتر IIR نمایش داده میشود. حروف بزرگ
برای فیلتر IIR نمایش داده میشود. حروف بزرگ ![]() و
و ![]() ، تعداد ضرایب فیلترها هستند که همچنین به آنها مرتبه یا تعداد نقاط فیلتر نیز گفته میشود. برای مثال، فیلتر FIR از
، تعداد ضرایب فیلترها هستند که همچنین به آنها مرتبه یا تعداد نقاط فیلتر نیز گفته میشود. برای مثال، فیلتر FIR از ![]() تا
تا ![]() عمل میکند.
عمل میکند.
– سری ![]() : خروجی گذشته زمانی در
: خروجی گذشته زمانی در ![]() ،
، ![]() ،
، ![]() ، …
، …
در عمل، فیلترهای FIR و IIR، تفاوتهای عملکردی مهمی دارند که در شکل ۸ به صورت خلاصه آمده است.

شکل ۸- خلاصه تفاوتهای بین فیلترهای FIR و IIR
فیلتر IIR دارای این مزیت است که نسبت به فیلتر FIR با فاکتور شیب ناحیه گذار یا roll-off مشابه، مرتبه پایینتر یا تعداد واحدهای فیلتر کمتری نیاز دارد. این بدان معنی است که محاسبات کمتری برای رسیدن به نتیجه مشابه، لازم دارد و به همین دلیل، فیلتر IIR را به لحاظ محاسباتی سریعتر میکند. هر چند که، فیلتر IIR، فاز غیرخطی دارد و با مسائل و مشکلات پایداری مواجه میشود. این مقایسه کمی مشابه مقایسه خرگوش و لاکپشت است. فیلتر FIR شبیه لاکپشت است که آرام و پیوسته عمل میکند و همیشه کار را تمام میکند. فیلتر IIR مشابه خرگوش است که خیلی سریع است ولی برخی اوقات دچار شکست میشود و نمیتواند مسابقه را تمام کند.
این تفاوتها با جزییات بیشتر در بخشهای بعدی بررسی میشوند.
۴- مرتبه فیلتر و سرعت محاسباتی
از فرمول مربوط به فیلتر FIR میتوان متوجه شد که هر چه عدد N بزرگتر باشد، مرتبه فیلتر نیز بالاتر میرود. برای مثال، اگر ۵ واحد در مقایسه با ۱۰ واحد در فیلتر وجود داشته باشد، محاسبات فیلتر در حالت دوم، دو برابر حالت اول خواهد بود. هر چند که، شیب ناحیه گذار فیلتر در حالت با مرتبه بیشتر، تندتر است (شکل ۹).

شکل ۹- شیب ناحیه گذار فیلتر با مرتبه کمتر (بالا)، کمتر از بخش مشابه در فیلتر با مرتبه بیشتر (پایین) است.
فیلتر با واحدهای بیشتر (مرتبه بالاتر)، ناحیه گذار تیزتری بین فرکانسهای عبوری و فرکانسهای متوقف شده دارد.
یک مثال که شامل فیلتر از یک نوع ولی با مرتبههای متفاوت است در زیر (شکل ۱۰) آمده است.

شکل ۱۰- افزایش مرتبه فیلتر و ثابت نگه داشتن بقیه مشخصات فیلتر، تیز بودن ناحیه گذار فیلتر یا roll-off یا افزایش میدهد.
با افزایش مرتبه فیلتر، به محاسبات بیشتر نیاز است و این مساله روی تاخیر ایجاد شده توسط فیلتر روی خروجی اثر میگذارد.
نکته: هر چه مرتبه فیلتر بیشتر باشد، فیلتر تیزتر است.
تیز بودن فیلترهای FIR و IIR با مرتبه فیلتر یکسان، بسیار متفاوت از یکدیگر است (شکل ۱۱)، زیرا فیلتر IIR به صورت بازگشتی عمل میکند که به معنی حضور بخشی از خروجی به عنوان ورودی فیلتر است که باعث میشود با مرتبه یکسان با فیلتر FIR، به فاکتور roll-off تیزتری دست یابد.

شکل ۱۱- با مرتبه یکسان، فیلتر IIR دارای فاکتور roll-off تیزتر نسبت به فیلتر FIR است.
به طور معکوس، تعداد واحدهای کمتری در فیلتر IIR برای دستیابی به عملکرد مشابه نسبت به فیلتر FIR، قابل استفاده است. این نکته در شکل ۱۲ نشان داده شده است.

شکل ۱۲- یک فیلتر IIR میتواند با مرتبه کمتر، به عملکرد یکسان با فیلتر FIR دست یابد.
این نکته، فیلتر IIR را از منظر محاسباتی، سریعتر از فیلتر FIR میسازد. معمولا برای پیادهسازی فیلتر به صورت زمان-واقعی (مثلا فیلتر کردن تعاملی در کاربردهای شنیداری) از ساختار IIR استفاده میشود. هر چند که، برخی ایرادهای بالقوه در استفاده از فیلتر IIR وجود دارد:
– تاخیر: فیلتر IIR دارای تاخیر غیریکسان در فرکانسهای مختلف است در حالیکه فیلتر FIR دارای یک تاخیر ثابت در هر فرکانس است.
– پایداری: با توجه به ساختار فیلتر IIR، این فیلتر برخی اوقات ناپایدار میشود و قابل استفاده و اعمال روی داده نخواهد بود. فیلتر FIR همیشه پایدار است.
نکته: برای مرتبه فیلتر یکسان، فیلتر IIR دارای فاکتور roll-off تیزتری نسبت به فیلتر FIR است.
۵- تاخیر زمانی و فیلترها
پس از اعمال فیلتر به داده زمانی و مقایسه آن با سری زمانی اصلی، یک جابهجایی یا تاخیر زمانی در داده قابل مشاهده است. در شکل ۱۳، دادههای همزمان دریافت شده صوت (منحنی قرمز در بالا) و ارتعاش (منحنی آبی در پایین) نشان داده شده است. فیلتر کردن داده صوتی (منحنی سبز در بالا) باعث میشود که اتفاقات رخ داده مابین صوت و ارتعاش در یک راستا نباشند.

شکل ۱۳- بالا: سیگنال زمانی اصلی (قرمز) توسط فیلتر دچار تاخیر زمانی میشود (سبز). پایین: سیگنال ارتعاش (آبی) با سیگنال صوت فیلتر شده (سبز) دیگر همراستا نیست.
چه چیزی باعث میشود که فیلتر در خروجی خود، تاخیر زمانی ایجاد کند؟
معادلات مربوط به فیلتر FIR در شکل ۱۴ را ببینید. با دنبال کردن معادلات، علت ایجاد تاخیر زمانی قابل مشاهده است:

شکل ۱۴- برای پیادهسازی کامل (کار کردن فیلتر به صورت واقعی)، فیلتر نیاز به تعداد نمونههایی به اندازه مرتبه خود برای عبور از آن دارد.
قبل از اینکه فیلتر شروع به کار کند، تعدادی نمونه داده زمانی سیگنال ورودی که متناسب با تعداد واحدهای فیلتر (N) است باید از فیلتر عبور کند. داده خروجی فیلتر شده تا قبل از اینکه این تعداد مشخص از داده عبوری از فیلتر بیشتر از N نشده است، شروع نمیشود.
چون بخشی از داده باید از فیلتر عبور کند تا خروجی تولید شود، یک تاخیر در خروجی زمانی در مقایسه با سیگنال ورودی ایجاد میشود. با باریکتر شدن ناحیه گذار فیلتر یا به عبارتی تیزتر شدن فیلتر، این تاخیر افزایش مییابد.
نکته: هر چه فیلتر تیزتر باشد، تاخیر زمانی آن طولانیتر است.
خصوصیات تاخیر یک فیلتر FIR و IIR همانطور که در شکل ۱۵ نشان داده شده است، بسیار متفاوت هستند.

شکل ۱۵- اندازه دامنه فیلترهای FIR و IIR (بالا) و تاخیر زمانی آنها (پایین). فیلتر FIR دارای تاخیر یکسان در تمامی فرکانسها است در حالیکه فیلتر IIR دارای تاخیر متغیر با فرکانس است.
نکته: فیلترهای FIR در تمامی فرکانسهای دارای تاخیر یکسان هستند در حالیکه فیلتر IIR دارای تاخیر زمانی متغیر در هر فرکانس است.
تمامی فیلترها – آنالوگ و دیجیتال – میزانی از تاخیر را ایجاد میکنند. بر اساس خصوصیات فیلتر، تاخیر میتواند کوتاهتر یا بلندتر باشد. همچنین این تاخیر میتوان به شکل تابعی متغیر از فرکانس نیز باشد.
۱-۵- فاز مستقیم در مقابل فاز صفر
تاخیر در سیگنال خروجی از طریق فیلتر کردن داده به صورت مستقیم و معکوس، قابل حذف است. بعد از اینکه سیگنال ورودی ![]() فیلتر شد و سیگنال خروجی
فیلتر شد و سیگنال خروجی ![]() تولید شد، این سیگنال را میتوان به صورت معکوس به فیلتر داد. برای این کار، دادههای
تولید شد، این سیگنال را میتوان به صورت معکوس به فیلتر داد. برای این کار، دادههای ![]() به لحاظ ترتیب زمانی معکوس شده و مجدد به فیلتر اعمال میشود. این کار را فیلتر کردن فاز صفر (zero phase filtering) میگویند. نتیجه در شکل ۱۶ آمده است.
به لحاظ ترتیب زمانی معکوس شده و مجدد به فیلتر اعمال میشود. این کار را فیلتر کردن فاز صفر (zero phase filtering) میگویند. نتیجه در شکل ۱۶ آمده است.
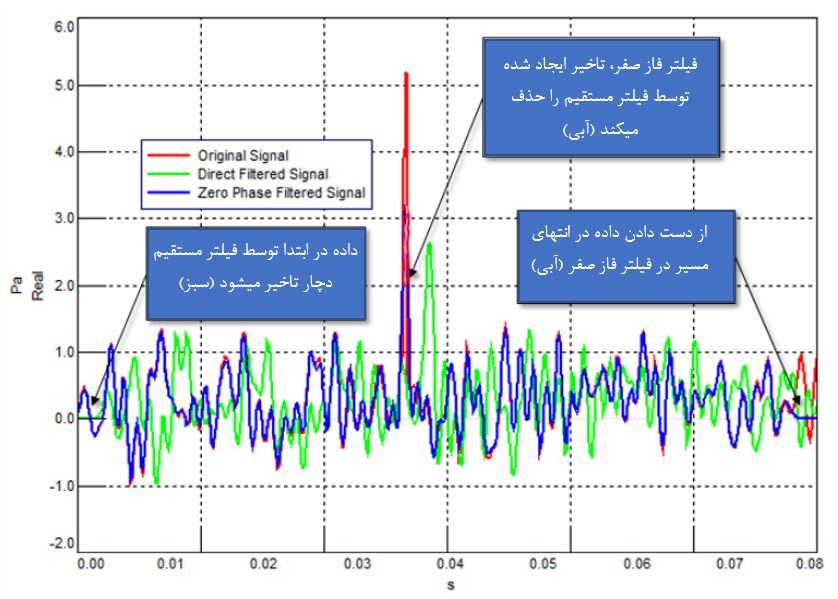
شکل ۱۶- سیگنال اصلی (قرمز) به صورت مستقیم فیلتر میشود (سبز) و همچنین به صورت فاز صفر (آبی). روش فاز صفر تاخیر را حذف میکند، اما داده در انتهای سیگنال زمانی فیلتر شده فاز صفر، از بین میرود. دقت کنید که تاخیر زمانی در انتهای مسیر داده فیلتر شده به روش فاز صفر (آبی) وجود دارد.
نه تنها خروجی فیلتر فاز صفر با ورودی در یک راستا قرار دارد بلکه داده نیز دو بار فیلتر شده است و به همین دلیل تضعیف ایجاد شده روی سیگنال دو برابر است. تعادلهایی در استفاده از فیلتر فاز صفر به شرح زیر وجود دارد:
– محاسبات نسبت به حالت عادی دو برابر زمان بیشتری میبرد.
– تنها در حالت داده دیجیتال به سادگی انجام میشود و برای سیگنالهای آنالوگ ساده نیست.
– داده در انتهای مسیر زمانی از بین میرود.
نکته: تاخیر و اثرات فازی توسط فیلتر کردن سری زمانی به روش مستقیم و معکوس (فاز صفر) قابل حذف است.
۶- روشهای طراحی فیلتر و ویژگیهای آنها
ضرایب فیلتر یا ![]() ، برای دستیابی به ویژگیهای مشخص آن، قابل انتخاب است. ضرایب یه به عبارتی روشهای طراحی آنها، مطابق شکل زیر بر روی ویژگیهای فیلتر اثر میگذارد.
، برای دستیابی به ویژگیهای مشخص آن، قابل انتخاب است. ضرایب یه به عبارتی روشهای طراحی آنها، مطابق شکل زیر بر روی ویژگیهای فیلتر اثر میگذارد.

شکل ۱۷- باندهای عبور، گذار و توقف در یک فیلتر
چهار ویژگی مهم در هر فیلتر وجود دارد که روشهای طراحی روی آنها تاثیر میگذارند:
– باند عبور: داده در باند عبور به طور مسقتیم به خروجی منتقل میشود. برای اطمینان از برابری داده عبوری از باند عبور با داده اصلی، نباید اعوجاج یا ریپل (ripple) در فیلتر وجود داشته باشد. ریپل یک نوع تغییرات دامنه به صورت تابعی از فرکانس در باندهای مختلف فیلتر است. به طور ایدهآل، در این باند، فیلتر باید دامنه با اندازه واحد داشته باشد.
– پهنای باند گذار: بر اساس کاربرد مورد نظر، ممکن است داشتن باند گذار بین دو باند عبور و توقف خیلی باریک بر حسب فرکانس، مورد نیاز باشد. هر دو فاکتور روش طراحی و مرتبه فیلتر، میزان سرعت عمل باند گذار را تعیین میکنند.
– باند توقف: در صورت وجود ریپل در این باند نیز امکان حضور داده فیلتر شده وجود دارد. در برخی کاربردها، ممکن است اندازه دامنه آنقدر کوچک باشد که این مساله چندان مهم نباشد. در برخی دیگر، حضور ریپل قابل قبول نیست.
– تاخیر گروهی/فاز: فیلترها در خروجی خود تاخیر ایجاد میکنند و این تاخیر میتواند متغیر با فرکانس باشد. همانطور که قبلا توضیح داده شد، اجرای عمل فیلتر کردن در دو مسیر رفت و برگشت (فیلتر فاز صفر) میتواند این تاخیر را از بین ببرد. در برخی کاربردها، که مساله فاز حیاتی است و روش فاز صفر به عنوان یک گزینه نمیتواند مطرح باشد، مساله فاز فیلتر یک نکته مهم در طراحی به شمار میرود.
۱-۶- روشهای طراحی فیلتر FIR
روشهای فیلتر با پاسخ ضربه محدود یا FIR در ادامه آمده و در شکل زیر نیز نشان داده شده است:

شکل ۱۸- روشهای فیلتر FIR
روشهای طراحی فیلتر FIR از پنجرههای طیفی مختلف در تبدیل از حوزه فرکانس به زمان استفاده میکنند. برخی از این روشها به شرح زیر است:
– چبیشف (Chebyshev): کمترین مقدار ریپل در باند توقف را دارد اما بیشترین عرض ناحیه گذار را نیز دارد.
– همینگ (Hamming): ناحیه گذار باریک، ریپل کمتر از روش هنینگ (Hanning)، توسط ریچارد همینگ ابداع شده که عضوی از پروژه منهتن بود.
– کایزر (Kaiser): توسط جمیز کایزر توسعه یافته است. پنجره کایزر دارای اندازه دامنه ریپل کم در ناحیه توقف است و ناحیه گذار عریض دارد.
– هنینگ (Hanning): باریکترین ناحیه گذار را دارد ولی ریپل ناحیه توقف زیاد است.
– مستطیلی (Rectangular): بیشترین مقدار ریپل و لوبهای فرعی را دارد که حتی روی باند عبور هم اثر میگذارد.
۲-۶- روشهای فیلتر IIR
روشهای طراحی فیلتر با پاسخ ضربه نامحدود یا IIR در شکل زیر آمده است:


شکل ۱۹- مقایسه فیلترهای IIR پایینگذر با مرتبه و فرکانس قطع (cutoff) یکسان
مشخصهات روشهای مختلف طراحی فیلتر IIR:
– باترورث (Butterworth): پاسخ صاف در هر دو باند عبور و توقف اما ناحیه گذار عریض دارد. اولین بار توسط فیزیکدان بریتانیایی، استفان باترورث (Stephen Butterworth) در ۱۹۳۰ معرفی شد.
– چبیشف معکوس (Inverse Chebyshev): پاسخ صاف در باند عبور و ناحیه گذار باریکتر نسبت به فیلتر باترورث دارد ولی در ناحیه توقف، ریپل دارد. اگر ریپل در ناحیه توقف از دید طراحی مسالهای ایجاد نکند، برای یک کاربرد خاص نسبت به فیلتر باترورث ارجحیت دارد.
– چبیشف (Chebyshev): در باند عبور ریپل دارد ولی شیب ناحیه گذار نسبت به روش چبیشف معکوس بیشتر است و ناحیه گذار باریکتر.
– کوئر (Cauer): باریکترین ناحیه گذار را دارد. در هر دو باند عبور و توقف ریپل دارد. برخی اوقات آن را فیلتر بیضوی (Elliptic filter) مینامند.
– بسل (Bessel): در هر دو باند عبور و توقف دارای دامنه شیبدار است و ناحیه گذار عریض دارد. تاخیر نسبت به فرکانس نسبت به بقیه روشها، صاف ترین حالت ممکن است. فیلتر بسل هم نام با ریاضیدان آلمانی، فردریچ بسل (Fredrich Bessel) انتخاب شده است.
نکته: روش طراحی فیلتر بر روی مشخصات مهم فیلتر همچون میزان ریپل و عرض ناحیه گذار، تاثیر میگذارد.
روش طراحی فیلتر بر اساس کابرد مورد نظر و داشتن بیشترین تطبیق با شرایط کار، انتخاب میشود.

دیدگاه ها (0)