توان و انرژی سیگنال
انرژی یک سیگنال
در پردازش سیگنال معمولا یک سیگنال به صورت تابعی از زمان در نظر گرفته میشود. عنوان “ اندازه و بزرگی یک سیگنال” برای نمایش میزان قدرت سیگنال استفاده میشود. دانستن اندازه یک سیگنال در برخی کاربردهای خاص بسیار مهم است. به طور مثال، ممکن است که بخواهیم میزان الکتریسیته لازم برای روشن کردن مانیتور LCD را در مقایسه با یک مانیتور CRT بدانیم. هر دو این کاربردها از یکدیگر متمایز بوده و میزان تلرانس متفاوتی دارند. بنابراین میزان الکتریسیته لازم برای به راه انداختن آنها نیز متفاوت است.
اندازه یک سیگنال به روشهای مختلفی قابل اندازهگیری و محاسبه است. اگر یک تابع ریاضی (یا یک سیگنال معادل آن) داده شده باشد، به نظر میرسد که مساحت زیر منحنی تابع، معیار مناسبی برای توصیف اندازه یک سیگنال باشد. یک سیگنال میتواند مقادیر مثبت و منفی داشته باشد. این موضوع باعث میشود که مساحت در برخی نواحی منفی نیز بشود. به همین دلیل، ممکن است که مقادیر محاسبه شده یکدیگر را به صورت جزیی یا کلی خنثی کرده و نتایج غلط به بار آورند. بنابراین معیار مورد نظر (مساحت زیر منحنی) برای تعریف اندازه یک سیگنال چندان مناسب نیست. حال با دو گزینه روبهرو هستیم: 1- محاسبه مساحت زیر منحنی مقدار مطلق تابع 2- محاسبه مساحت زیر منحنی مربع تابع. گزینه دوم به دلیل قابلیت ردیابی و کنترل ریاضی بهتر و شباهت آن به نُرم اقلیدسی که در روشهای تشخیص سیگنال به کار میرود، مناسبتر است. (نُرم اقلیدسی یا همان L2، اغلب در روشهای تشخیص سیگنال به کار میرود زیرا این روش معیاری از فاصله بین دو نقطه در فضای سیگنالی است و در تئوری تخمین تحت عنوان فاصله اقلیدسی شناخته میشود).
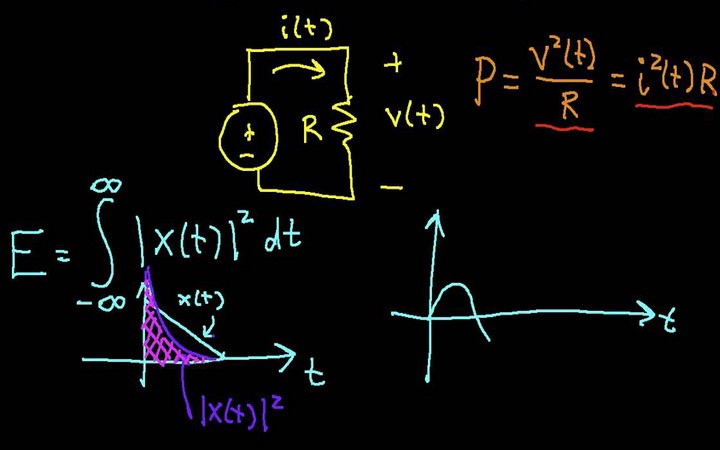
با توجه به انتخاب دوم و در نظر گرفتن اندازه سیگنال به شکل محاسبه مساحت زیر منحنی مربع تابع، انرژی سیگنال زمانپیوسته و مختلط (x(t به صورت زیر تعریف میشود:
پارامتر در پردازش سیگنال، انرژی سیگنال نام دارد. همچنین معیاری از قدرت سیگنال است. این تعریف به هر نوع سیگنال (یا بردار) فارغ از اینکه حامل انرژی باشد یا نباشد، قابل اعمال است. اگر سیگنال مورد نظر مربوط به انرژی فیزیکی خاصی باشد، عبارت بالا محتوای انرژی سیگنال را بدست میآورد. اگر سیگنال از نوع الکتریکی باشد، تعریف بالا انرژی کل سیگنال که بر روی یک مقاومت یک اهمی هدر داده میشود را محاسبه میکند.
انرژی واقعی – مقدار فیزیکی
برای دانستن میزان انرژی سیگنال، E، باید مقدار باری (Z) که سیگنال در حال تغذیه آن است و همچنین نوع سیگنال الکتریکی (ولتاژ یا جریان) مشخص باشد. برای سیگنال ولتاژ، معادله بالا با فاکتور میتواند تغییر مقیاس داده شود.
برای سیگنال جریان، تغییر مقیاس با Z انجام میشود.
در اینجا، Z امپدانس تحریک شده با سیگنال (x(t است، Ex انرژی سیگنال است و E انرژی سیگنالی است که بار Z را تحریک میکند.
انرژی در حوزه زمانگسسته
در حوزه گسسته، انرژی سیگنال به شکل زیر محاسبه میشود:
اگر مجموع بالا به یک مقدار محدود همگرا شود، انرژی سیگنال نیز محدود خواهد بود. به عبارت دیگر سیگنال به صورت جمع پذیر مربعی است. چنین سیگنالی را سیگنال انرژی گویند.
اگر این جمع برای یک سیگنال در طول زمان کاهش نیابد (همچون موج سینوسی پیوسته که تا بینهایت سیکل تکراری ایجاد میکند) چه اتفاقی خواهد افتاد؟ انرژی بینهایت میشود و چنین سیگنالی جمعپذیر مربعی نیست. برای رفع این مشکل، نیاز به معیار اندازهگیری دیگری داریم. این موضوع ما را به مفهوم توان سوق میدهد.
توان
توان به صورت مقدار انرژی مصرف شده در واحد زمان تعریف میشود. این کمیت در شرایطی که انرژی سیگنال به بینهایت میل میکند یا اصطلاحا سیگنال جمعپذیر مربعی نباشد، مفید است. برای سیگنالهای جمعناپذیر مربعی، توان با استفاده از محتوای سیگنال در بازه زمانی مشخصی به شکل زیر محاسبه میشود:
- یک بخش از سیگنال بر روی بازه زمانی محدودی در نظر گرفته شود
- انرژی این سیگنال محاسبه شود
- انرژی به تعداد نمونههای گرفته شده برای محاسبه تقسیم شود
- حد تعداد نمونهها به بینهایت گسترش داده شود. با این کار توان کل سیگنال محاسبه میشود.
در حوزه زمانگسسته، توان کل سیگنال به صورت زیر محاسبه میشود:
معادلاتی که در ادامه آمده است، روشهای مختلف محاسبه توان است که در کتابهای مختلف ارائه شده است. تنها تفاوت در تعداد نمونهها برای محاسبه است. مخرج کسر بر اساس تعداد نمونههای گرفته شده برای محاسبه توان، تغییر میکند.
کلاسبندی سیگنالها
یک سیگنال بر اساس محتوای توان یا انرژی آن میتواند دستهبندی شود. سیگنالهایی که انرژی محدود دارند، سیگنال انرژی هستند و سیگنالهای توان نیز سیگنالهای با توان محدود و غیرصفر هستند.
سیگنال انرژی
یک سیگنال با انرژی محدود، دارای توان کل صفر است. بیایید این عبارت را با جزییات بیشتری بررسی کنیم. زمانیکه انرژی محدود است، توان کل صفر میشود. اگر مخرج کسری که در معادله توان کل وجود دارد را دقیقتر نگاه کنیم، متوجه میشویم که با میل کردن N به بینهایت، انرژی بر روی محدوده زمانی مورد نظر به صفر نزدیک میشود و در نتیجه توان کل نیز صفر میشود.
سیگنال توان
سیگنالهایی که توان کل آنها محدود است را سیگنال توان میگویند. انرژی سیگنال توان نیز بینهایت خواهد بود. مثال: دنبالههای متناوب همچون سینوسی. یک سیگنال سینوسی توان محدود و غیرصفر دارد ولی انرژی آن نامحدود است.
یک سیگنال به طور همزمان نمیتواند سیگنال انرژی و سیگنال توان باشد.
سیگنالی که نه انرژی است و نه توان
سیگنال با دامنه افزایشی زیر را در نظر بگیرید:
برای چنین سیگنالی، هر دو مقدار انرژی و توان، نامحدود است. بنابراین نمیتواند به عنوان یک سیگنال انرژی یا توان دستهبندی شود.
منبع: www.gaussianwaves.com

دیدگاه ها (0)