اهمیت مقدار موثر یا جذر میانگین مربعات (RMS)
تعریف مفهوم “اندازه سیگنال”
معمولا یک سیگنال در کاربردهای مختلف پردازش سیگنال به صورت تابعی از زمان در نظر گرفته میشود. عبارت “اندازه یک سیگنال” برای نشان داده قدرت سیگنال استفاده میشود. لازم به ذکر است که اندازه سیگنال در برخی کاربردهای خاص مورد استفاده قرار میگیرد. به طور مثال، ممکن است علاقمند باشیم که بدانیم میزان توان الکتریکی لازم برای روشن کردن مانیتور LCD در مقایسه با CRT چقدر است. چون با کاربردهای مختلفی روبرو هستیم بنابراین میزان الکتریسیته لازم برای فعال کردن آنها نیز متفاوت است.
اندازه یک سیگنال به روشهای مختلفی قابل اندازهگیری است. برخی از آنها عبارت است از:
- انرژی کل
- جذر مربعی مقدار مطلق
- مقدار مطلق انتگرال
- مقدار مطلق ماکزیمم یا حداکثر
- مقدار جذر میانگین مربعات یا RMS
- مقدار متوسط مطلق یا AA
مقدار RMS
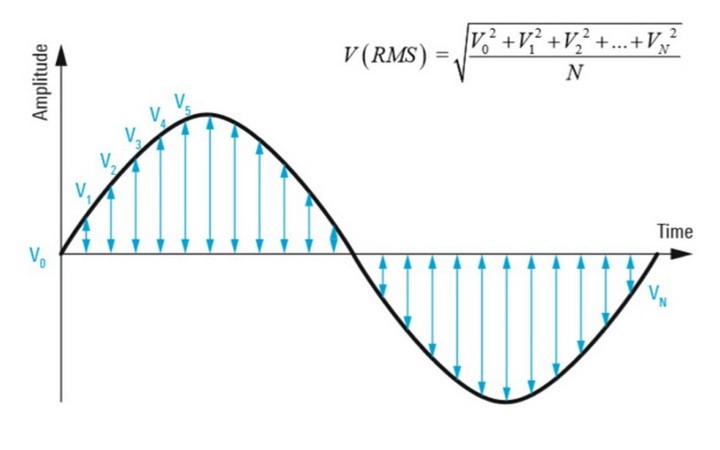
مقدار RMS یک سیگنال (به طور مثال ) به صورت جذر ریشه دوم مقدار متوسط مقادیر مربع سیگنال محاسبه میشود که فرمول ریاضی آن به شکل زیر است:
برای سیگنال گسسته با N مقدار متمایز نیز، مقدار RMS به فرم زیر محاسبه میشود:
اگر سیگنال به صورت در حوزه فرکانس قابل نمایش باشد، بر اساس تئوری پارسوال، مقدار RMS به این شکل قابل محاسبه است:
پیادهسازی در متلب:
N=100; %length of the signal
x=randn(1,N); %a random signal to test
X=fft(x); %Frequency domain representation of the signal
RMS1 = sqrt(mean(x.^2)) %RMS value from time domain samples
RMS2 = sqrt(sum(abs(X/N).^2)) %RMS value from frequency domain representation
Result: RMS1 – RMS2 = 1.1102e-16
اهمیت مقدار RMS
مقدار RMS یکی از مهمترین پارامترهایی است که در توصیف قدرت جریان متناوب (AC) استفاده میشود. مقدار RMS یک ولتاژ یا جریان AC معادل جریان یا ولتاژ DC است که اثر حرارتی مشابهی را در حین اعمال به دو سر مقاومت یکسان، ایجاد میکند. بنابراین، معیاری از محتوای انرژی سیگنال داده شده نیز هست.
در آمار، برای هر متغیر تصادفی ایستان با میانگین صفر، مقدار RMS برابر است با مقدار انحراف معیار سیگنال. به طور مثال در توزیع تاخیر در یک کانال چند مسیره با استفاده از مقدار RMS پروفایل تاخیر توان (PDP) محاسبه میشود.
زمانیکه دو سیگنال ناهمبسته (یا متعامد) با هم جمع میشوند، همچون سیگنالهای نویزی که از دو منبع مستقل تولید شدهاند، مقدار RMS جمع آنها برابر است با جذر جمع مربع RMS آنها.
منبع: www.gaussianwaves.com

دیدگاه ها (0)