آشنایی با متغیرهای تصادفی و توزیع‌های احتمال

 

 

تئوری احتمال، شاخه‌ای از ریاضیات است که درگیر مطالعه پدیده‌های تصادفی است و اغلب به عنوان یکی از پایه‌های اصلی یادگیری ماشین، در نظر گرفته میشود. هر چند که، یک مبحث بسیار گسترده است و به سادگی میتوان در آن سردرگم شد، به خصوص زمانی که بخواهیم خودآموزی انجام دهیم.

در بخشهایی که در ادامه می‌آیند، میخواهیم برخی جنبه‌های اساسی مرتبط با یادگیری ماشین، یعنی متغیر تصادفی (Random Variable – RV) و توزیع احتمال (Probability Distribution) را پوشش دهیم.

قبل از این که مستقیم وارد عمق تئوری احتمال شویم، بهتر است که به دنبال پاسخ به این سوال باشیم که اصولا چرا این مفاهیم برای یادگیری مهم هستند و چرا در وحله اول باید به آنها توجه کنیم.

 

 

چرا احتمال؟

 

در یادگیری ماشین، اغلب با عدم قطعیت (Uncertainty) و مقادیر تصادفی مواجه می‌شویم که به دلیل مشاهده ناقص داده است و به همین علت بسیار محتمل است که با داده نمونه‌برداری شده، کار کنیم.

حال فرض کنید که میخواهیم نتایج قابل اتکایی درباره رفتار یک متغیر تصادفی، بدست آوریم علی‌رغم اینکه داده محدودی در دسترس داریم و درباره کل جمعیت داده، اطلاع نداریم.

بنابراین، به روشی نیاز داریم که بتواند داده نمونه‌برداری شده محدود را به کل جمعیت، تعمیم دهد یا به زبان دیگر، نیاز داریم تا فرآیند تولید داده واقعی را تخمین بزند.

 

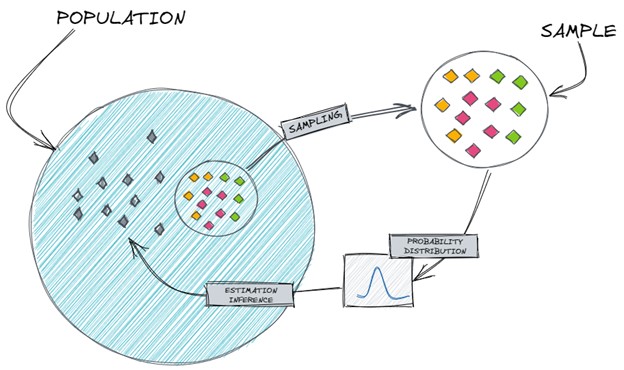
شکل 1- تخمین فرآیند تولید داده

 

درک و فهم توزیع احتمال، به ما این امکان را میدهد که احتمال یک پیشامد مشخص را با احتساب تغییرات محتمل در نتایج، محاسبه کنیم. بدین ترتیب، این ابزار امکان تعمیم از نمونه‌ها به جمعیت کل را فراهم میکند، تابع مولد داده را تخمین میزند و رفتار یک متغیر تصادفی را به طور دقیق‌تر، پیش‌بینی میکند.

 

 

معرفی متغیر تصادفی

 

به زبان ساده، متغیر تصادفی، یک متغیر است که مقدار آن وابسته به نتیجه یک رخداد تصادفی است. همچنین میتوان آن را به شکل یک تابع توصیف کرد که از فضای نمونه به فضای قابل اندازه‌گیری (به شکل یک عدد واقعی) نگاشت می‌یابد.

بیایید فرض کنیم، یک فضای نمونه شامل 4 دانش‌آموز داریم: {A, B, C, D}. اگر به طور تصادفی دانش آموز A را انتخاب کنیم و قد او را به سانتی‌متر اندازه‌گیری کنیم، میتوان متغیر تصادفی (H) را به شکل یک تابع با ورودی دانش‌آموز و خروجی قد او به صورت یک عدد حقیقی، در نظر گرفت:

 

    \[ H(student) = height (in \ cm) \]

 

میتوانیم این مثال ساده را به شکل زیر، تصور کنیم:

 

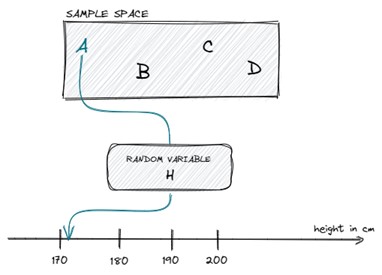
شکل 2- مثالی از یک متغیر تصادفی

 

بر اساس نتیجه (کدام دانش‌آموز به طور تصادفی انتخاب شود)، متغیر تصادفی ما (H ) میتواند حالتها یا مقادیر مختلفی بر حسب قد به سانتی‌متر، داشته باشد.

 

نکته: یک متغیر تصادفی میتواند گسسته (Discrete) یا پیوسته (Continuous) باشد.

 

اگر متغیر تصادفی ما، فقط تعداد محدود و یا تعداد قابل شمارشی از مقادیر متمایز نامحدود را بتواند اختیار کند، یک متغیر تصادفی گسسته است. مثالهایی از متغیر تصادفی گسسته شامل تعداد دانش‌آموزان در یک کلاس، سوالهای تستی درست پاسخ داده شده در یک آزمون، تعداد فرزندان در یک خانواده و … است.

از طرفی دیگر، متغیر تصادفی ما پیوسته است اگر بین هر دو مقدار آن، تعداد نامحدودی از مقادیر مجاز برای آن متغیر تصادفی، وجود داشته باشد. مقادیری همچون فشار، قد، وزن و فاصله را میتوان مثالهایی از متغیرهای تصادفی پیوسته به شمار آورد.

زمانیکه متغیر تصادفی را با یک توزیع احتمال تلفیق میکنیم، در واقع به این سوال پاسخ میدهیم: چقدر محتمل است که متغیر تصادفی ما یک مقدار مشخص را داشته باشد؟ که اصولا معادل آن است که در مورد احتمال رخداد سوال کنیم.

حال فقط یک سوال باقی میماند: توزیع احتمال چیست؟

 

 

توزیع احتمال

 

توصیف اینکه چقدر محتمل است که یک متغیر تصادفی یکی از حالتها یا مقادیر ممکن خود را اتخاذ کند، توسط توزیع احتمال قابل ارائه است. بنابراین، توزیع احتمال یک تابع ریاضی است که احتمالهای نتایج مختلف را برای یک آزمون تصادفی به ما میدهد.

به طور عام‌تر میتوان گفت که توزیع احتمال به صورت یک تابع که در زیر آمده است، قابل بیان است:

 

    \[ P: \ A \rightarrow \mathbb{R} \]

 

که فضای ورودی A – مرتبط با فضای نمونه – را به یک عدد حقیقی، نگاشت میدهد که همان احتمال رخداد مورد نظر است.

 

برای اینکه تابع بالا، یک توزیع احتمال را مشخص کند، باید از اصول کولموگروف (Kolmogrov) پیروی کند:

 

– نامنفی بودن

– از مقدار یک فراتر نرود

– جمع‌پذیر بودن هر رخداد قابل شمارش مجزا (انحصاری متقابل – mutually exclusive)

 

 

روشی که یک توزیع احتمال را بوسیله آن توصیف میکنیم، به گسسته یا پیوسته بودن متغیر تصادفی وابسته است که در نتیجه آن تابع جرم احتمال (Probability Mass Function – PMF) یا تابع چگالی احتمال (Probability Density Function – PDF) خواهیم داشت.

 

 

تابع جرم احتمال

 

تابع جرم احتمال یا همان PMF، توزیع احتمال روی یک متغیر تصادفی گسسته را توصیف میکند. به عبارت دیگر، PMF تابعی است که احتمال اینکه یک متغیر تصادفی، دقیقا برابر با یک مقدار مشخص باشد را برمیگرداند.

احتمال برگشتی از سمت تابع PMF در محدوده [0, 1] قرار دارد و جمع تمام احتمالها برای تمام حالتهای ممکن متغیر تصادفی، برابر با یک خواهد بود.

نموداری را فرض کنید که محور x آن حالتها را نشان میدهد و محور y، احتمال یک حالت خاص را مشخص میکند. تصور نمودار به این شکل، به ما این امکان را میدهد که احتمال یا PMF را به صورت یک نمودار میله‌ای به شکل زیر تصور کنیم:

 

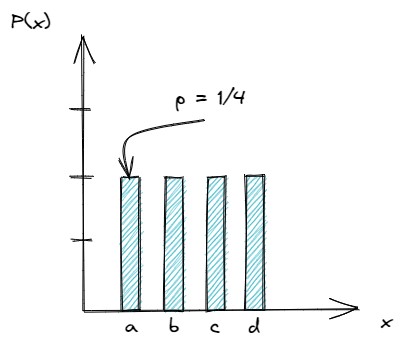
شکل 3- مثالی از PMF ( به صورت یکنواخت)

 

در ادامه، سه توزیع احتمال گسسته مرسوم را بررسی میکنیم: توزیع برنولی (Bernoulli)، توزیع دو جمله‌ای (Binomial) و توزیع هندسی (Geometric)

 

 

توزیع برنولی

 

بعد از انتخاب نام ریاضیدان مشهور سوییسی، ژاکوب برنولی، برای این توزیع احتمال، توزیع برنولی، یک توزیع احتمال گسسته از متغیر تصادفی تکی باینری که یکی از دو مقدار صفر یا یک را اختیار میکند، معرفی شد.

به زبان ساده، توزیع برنولی را میتوان مدلی فرض کرد که نتایج ممکن برای یک آزمایش تکی را بدست میدهد که نتیجه هر آزمایش با یک سوال بله-خیر قابل پاسخ‌دهی است.

به زبان ریاضی، تابع احتمال به شکل معادله زیر قابل تعریف است:

 

    \[ \begin{aligned} f(k; p) = \begin{cases} q=1-p \ \ \ if k=0 \\ p \ \ \ \ \ \ \ \ \ \ \ \ \ \ if k=1 \end{cases}\\ \\ f(k; p) = p^k (1-p)^{1-k} \ \ \ \ for \ k \in [0,1] \end{aligned} \]

 

که اصولا مقدار آن p است، اگر k=1 و 1-p است، اگر k=0. بنابراین، توزیع برنولی تنها با یک پارامتر p، مشخص میشود. 

فرض کنید که یک سکه متقارن را یکبار پرتاب کنیم. احتمال اینکه شیر بیابد برابر با \frac{1}{2} خواهد بود. نمایش PMF این توزیع احتمال، به شکل زیر خواهد بود:

 

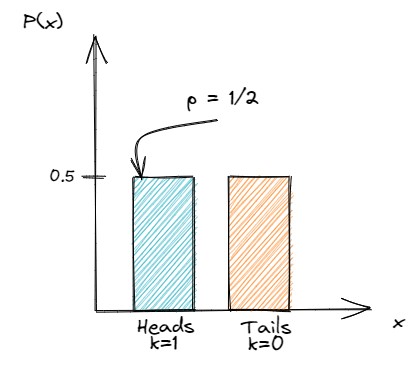
شکل 4- مثالی از آزمون برنولی

 

 

نکته: توزیع برنولی مقدار صفر یا یک را اختیار میکند، که آن را به طور ویژه‌ای برای نمایش یک متغیر نامی یا دو حالته، مناسب میسازد. 

 

از آنجاییکه توزیع برنولی تنهای یک آزمون تکی را مدل میکند، میتواند یک حالت خاص از توزیع دو جمله‌ای نیز، در نظر گرفته شود.

 

 

توزیع دو جمله‌ای

 

توزیع دو جمله‌ای یک توزیع احتمال گسسته از تعداد دفعات موفقیت در دنباله‌ای از n آزمون مستقل را توصیف میکند که هر آزمون یک نتیجه باینری دارد. موفقیت یا شکست به ترتیب با  احتمالهای p و 1-p داده میشود. 

بنابراین، توزیع دو جمله‌ای به صورت زیر توسط پارامترها تعریف میشود:

 

    \[ n \in \mathbb{N}, \ \ p \in [0,1] \]

 

به زبان رسمی‌تر، توزیع دو جمله‌ای میتواند توسط معادله زیر نیز بیان شود:

 

    \[ f(k; n, p) = \binom{n}{k} p^k (1-p)^{n-k} \]

 

احتمال موفقیت به تعداد k با توان k-ام p داده شده و احتمال شکست نیز با توان (n-k) – ام مقدار 1-p تعریف شده است.

از آنجاییکه رخدادهای موفقیت‌آمیز، هر جایی در کل n آزمون میتواند اتفاق بیفتد، به تعداد انتخاب k از n حالت ممکن، راه برای توزیع موفقیت‌آمیز وجود دارد. حال بیایید مثال پرتاب سکه را که قبلا بررسی کردیم، برای این توزیع به کار ببریم. 

در اینجا میخواهیم سکه را سه بار پرتاب کنیم که در آن، متغیر تصادفی تعداد شیر آمدن سکه‌ها را توصیف میکند.

 

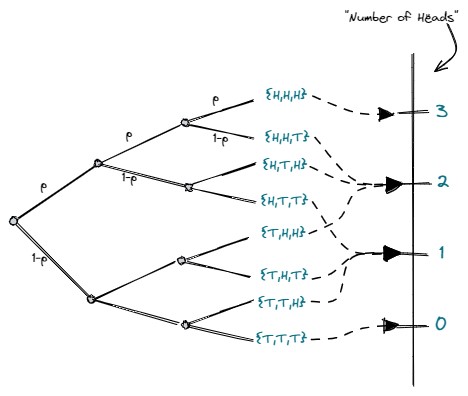
شکل 5- تعداد شیر آمدن در سه بار پرتاب سکه

 

اگر بخواهیم احتمال اینکه در این سه پرتاب، دو بار شیر بیاید را حساب کنیم، میتوانیم به سادگی از معادله زیر استفاده کرده و مقدار احتمال را بدست آوریم:

 

    \[ \begin{aligned} P(2) = \binom{3}{2} p^2 (1-p)^{3-2} \\ \\ P(2) = 3(0.5)^2(0.5)^1 \\ \\ P(2) = 0.375 \end{aligned} \]

 

اگر به همین شکل برای سایر احتمالها، عمل کنیم، نمودار زیر را برای توزیع احتمال بدست می‌آوریم:

 

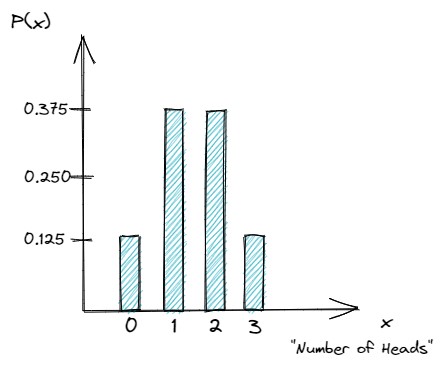
شکل 6- توزیع دو جمله‌ای سه بار پرتاب سکه

 

 

توزیع هندسی

 

فرض کنید که میخواهیم تعداد دفعات لازم برای پرتاب یک سکه تا آمدن اولین شیر را محاسبه کنیم. توزیع هندسی، احتمال اولین رخداد موفقیت‌آمیز را که نیاز به n آزمون مستقل دارد به صورت احتمال p به ما میدهد. 

به زبان ریاضی، میتوان نوشت:

 

    \[ P(n) = (1-p)^{n-1} p \]

 

که  احتمال تعداد دفعات لازم برای رسیدن به اولین رخداد موفقیت‌آمیز را محاسبه میکند.

به منظور محاسبه توزیع هندسی، فرضیات زیر باید برقرار باشند:

 

– مستقل بودن

– در هر آزمون، تنها دو حالت یا نتیجه ممکن وجود دارد (در مثال پرتاب سکه: شیر یا خط)

– احتمال موفقیت در هر آزمون یکسان است

 

 

اجازه دهید تا توزیع هندسی را که پاسخ به این سوال است که چند دفعه باید آزمون سکه تکرار شود تا به رخداد موفقیت‌آمیز دست یابیم، را با رسم شکل نشان دهیم:

 

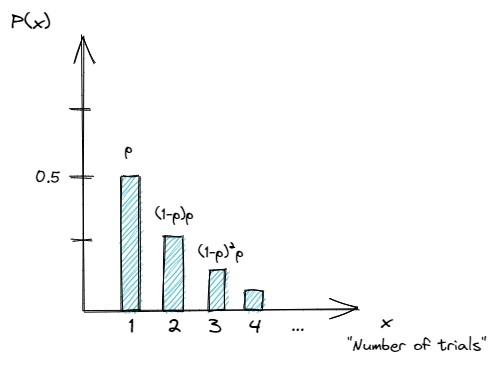
شکل 7- توزیع هندسی تا رسیدن به اولین شیر در پرتاب سکه

 

 

تابع چگالی احتمال

 

در بخشهای قبل، متوجه شدیم که یک متغیر تصادفی میتواند گسسته یا پیوسته باشد. اگر گسسته باشد، توزیع احتمال توسط تابع جرم احتمال توصیف میشود. 

حال، با متغیر تصادفی پیوسته کار داریم و به همین دلیل برای توصیف کردن توزیع احتمال به تابع چگالی احتمال یا PDF نیاز داریم. 

PDF برخلاف PMF، احتمال اینکه یک متغیر تصادفی، مقدار مشخصی را اتخاذ کند، نمیدهد. به جای آن، این تابع، احتمال اینکه متغیر تصادفی در یک ناحیه مشخص قرار گیرد را تعیین میکند. به زبان دیگر، PDF احتمال اینکه متغیر تصادفی داخل یک محدوده مشخص از مقادیر قرار گیرد، را توصیف میکند. 

به منظور یافتن جرم احتمال واقعی، باید انتگرال‌گیری انجام دهیم که در واقع مساحت زیر تابع چگالی را از محور x به بالا محاسبه میکند. 

 

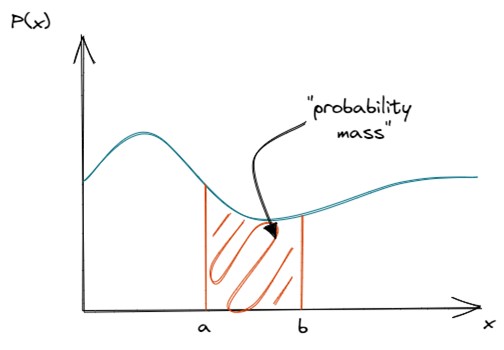
شکل 8- مثالی از تابع چگالی احتمال

 

تابع چگالی احتمال، باید غیرمنفی باشد و انتگرال کل آن برابر با یک باشد:

 

    \[ (1) \ \ p(x) \ge 0 \\ \]

 

    \[ \(2) \int p(x) \delta x=1 \]

 

 

منبع: https://towardsdatascience.com